Energy Conservation

This example demonstrates the energy conservation of a single particle motion in three cases.

1. Constant B field, Zero E field.

2. Constant E field, Zero B field.

3. Magnetic Mirror.

The tests are performed in dimensionless units with q=1, m=1. We compare multiple solvers: Tsit5, Vern7, Vern9, BS3, ImplicitMidpoint, Boris, and Boris Multistep.

using TestParticle
using TestParticle: ZeroField
using OrdinaryDiffEq
using StaticArrays
using LinearAlgebra: ×, norm
using CairoMakie

const q = 1.0
const m = 1.0
const B₀ = 1.0
const E₀ = 1.0
const Ω = q * B₀ / m
const T = 2π / Ω

# Helper function to run tests
function run_test(
        case_name, param, x0, v0, tspan, expected_energy_func;
        uselog = true, dt = 0.1, ymin = nothing, ymax = nothing
    )
    u0 = [x0..., v0...]
    prob_ode = ODEProblem(trace_normalized!, u0, tspan, param)
    prob_tp = TraceProblem(u0, tspan, param)

    f = Figure(size = (1000, 600), fontsize = 18)
    if uselog
        yscale = log10
    else
        yscale = identity
    end

    ax = Axis(
        f[1, 1],
        title = "$case_name: Energy Error",
        xlabel = "Time",
        ylabel = "Rel. Energy Error |(E - E_ref)/E_ref|",
        yscale = yscale
    )

    if !isnothing(ymin) && !isnothing(ymax)
        ylims!(ax, ymin, ymax)
    end
    function plot_energy_error!(sol, label, marker)
        # Calculate energy
        v_mag = [norm(u[4:6]) for u in sol.u]
        E = 0.5 .* m .* v_mag .^ 2

        # Expected energy
        t = sol.t
        x = @views [u[1:3] for u in sol.u]
        # Pass velocity to expected_energy_func just in case
        E_ref = @views [
            expected_energy_func(ti, xi, u[4:6])
                for (ti, xi, u) in zip(t, x, sol.u)
        ]

        # Error (Avoid division by zero if E_ref is 0)
        error = abs.(E .- E_ref) ./ (abs.(E_ref) .+ 1.0e-16)

        return scatter!(ax, t, error, label = label, marker = marker)
    end

    # Run ODE solvers
    for (name, alg, marker) in ode_solvers
        sol = solve(prob_ode, alg; adaptive = false, dt, dense = false)
        plot_energy_error!(sol, name, marker)
    end

    # Run native solvers
    for (name, marker, kwargs) in native_solvers
        sol = TestParticle.solve(prob_tp; dt, kwargs...)[1]
        plot_energy_error!(sol, name, marker)
    end

    f[1, 2] = Legend(f, ax, "Solvers", framevisible = false, labelsize = 24)

    return f
end

# Solvers to test
const ode_solvers = [
    ("Tsit5", Tsit5(), :circle),
    ("Vern7", Vern7(), :rect),
    ("Vern9", Vern9(), :diamond),
    ("BS3", BS3(), :utriangle),
    ("ImplicitMidpoint", ImplicitMidpoint(), :pentagon),
]

const native_solvers = [
    ("Boris", :star5, Dict{Symbol, Any}()),
    ("Boris Multistep (n=2)", :star8, Dict{Symbol, Any}(:n => 2)),
];

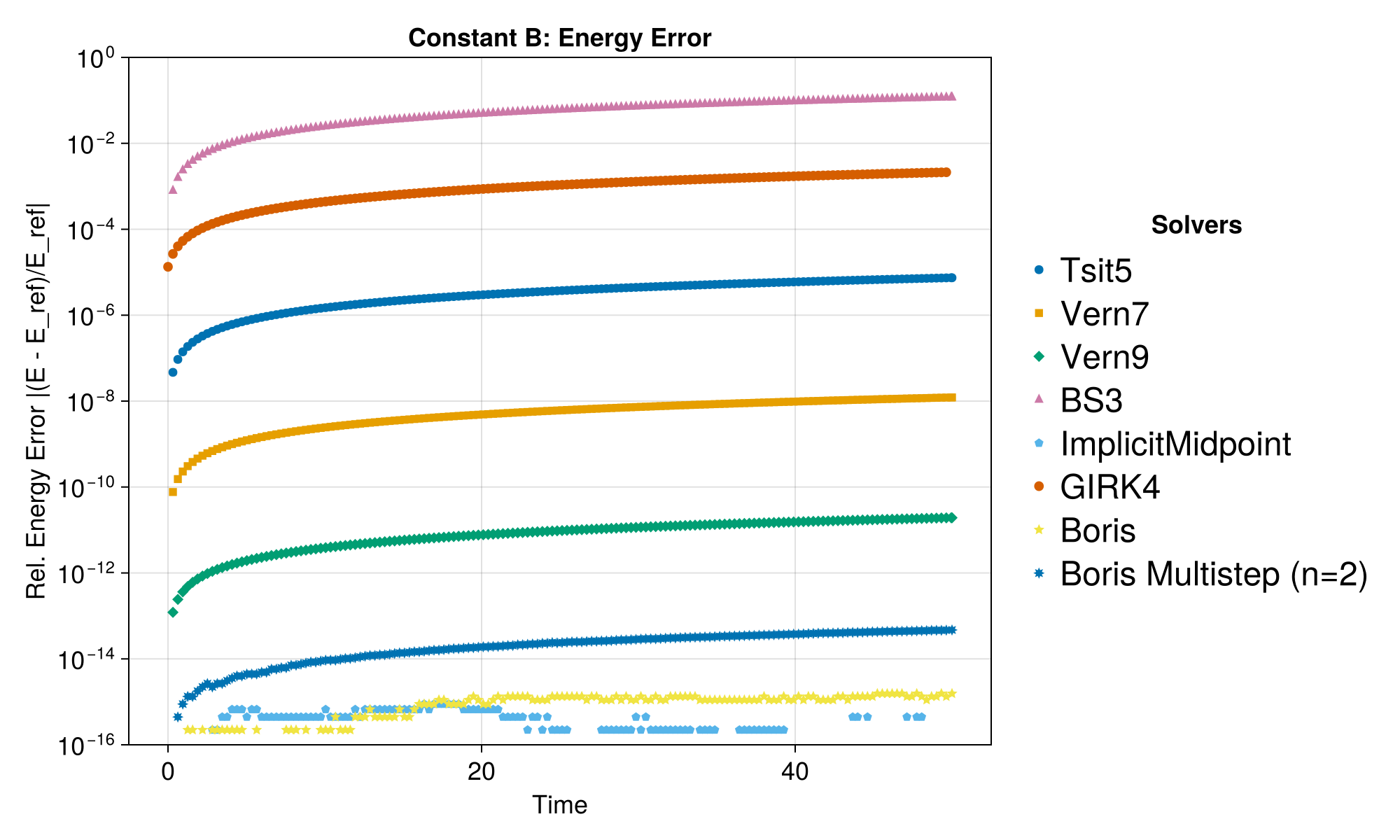
Case 1: Constant B, Zero E

Energy should be conserved.

uniform_B(x) = SA[0, 0, B₀]

param1 = prepare(ZeroField(), uniform_B; q = q, m = m)
x0_1 = [0.0, 0.0, 0.0]
v0_1 = [1.0, 0.0, 0.0]
tspan1 = (0.0, 50.0)
E_func1(t, x, v) = 0.5 * m * norm(v0_1)^2 # Constant energy

f = run_test(
    "Constant B", param1, x0_1, v0_1, tspan1, E_func1; dt = T / 20, ymin = 1.0e-16, ymax = 1.0
)

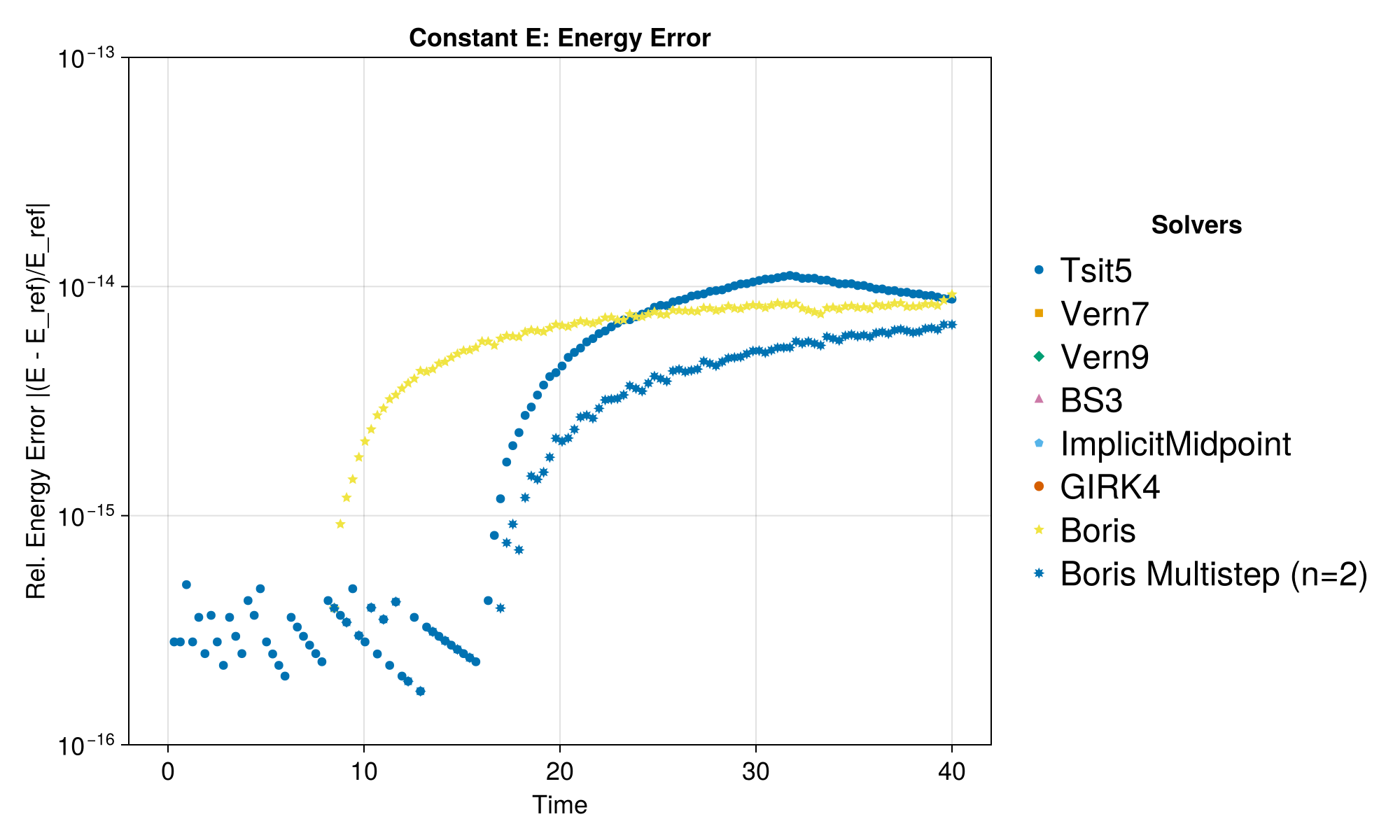
Case 2: Constant E, Zero B

Energy increases due to work done by the electric field. For a particle starting from rest in constant E field:

$$\begin{array}{rl}\mathbf{a}& =\frac{q}{m}\mathbf{E}\\ \mathbf{v}(t)& =\mathbf{a}t(\mathrm{if}{v}_0=0)\end{array}$$$$E_{kin}=\frac{1}{2}m{v}^2=\frac{1}{2}m(\frac{q{E}_0}{m}t{)}^2$$

constant_E(x, t) = SA[E₀, 0.0, 0.0]

param2 = prepare(constant_E, ZeroField(); q = q, m = m)
x0_2 = [0.0, 0.0, 0.0]
v0_2 = [0.0, 0.0, 0.0] # Start from rest
tspan2 = (0.0, 40.0)

function E_func2(t, x, v)
    v_theo = (q * E₀ / m) * t # analytical energy
    return 0.5 * m * v_theo^2
end

f = run_test(
    "Constant E", param2, x0_2, v0_2, tspan2,
    E_func2; dt = T / 20, ymin = 1.0e-16, ymax = 1.0e-13
)

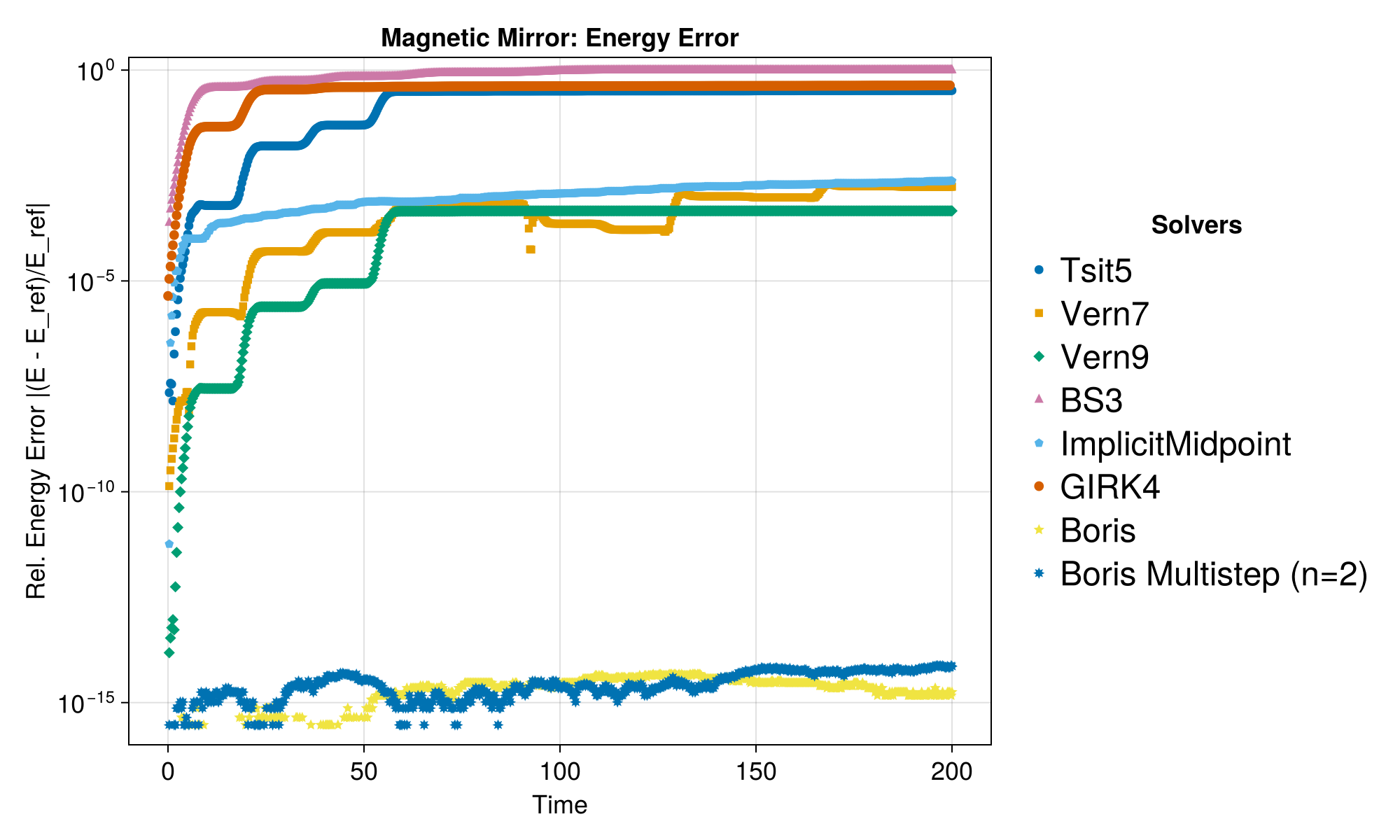
Case 3: Magnetic Mirror

Energy should be conserved (E=0). The particle bounces back and forth between regions of high magnetic field. We set a divergence-free B field in cylindrical symmetry

$$\begin{array}{rl}{B}_x& =-\alpha B_{0}xz\\ B_y& =-\alpha B_{0}yz\\ B_z& =B_0(1+\alpha z^2)\end{array}$$

function mirror_B(x)
    α = 0.1
    Bz = B₀ * (1 + α * x[3]^2)
    Bx = -B₀ * α * x[1] * x[3]
    By = -B₀ * α * x[2] * x[3]
    return SA[Bx, By, Bz]
end

param3 = prepare(ZeroField(), mirror_B; q = q, m = m)
x0_3 = [0.1, 0.0, 0.0]
v0_3 = [0.5, 0.5, 1.0]
tspan3 = (0.0, 200.0)
E_init_3 = 0.5 * m * norm(v0_3)^2
E_func3(t, x, v) = E_init_3

f = run_test(
    "Magnetic Mirror", param3, x0_3, v0_3, tspan3, E_func3;
    dt = T / 20, ymin = 1.0e-16, ymax = 2.0
)