Cosmic Ray

This example shows how to trace cosmic rays in a background magnetic field. In the original MHD solution, everything is dimensionless. We are following the normalization procedures in Cosmic ray propagation in sub-Alfvénic magnetohydrodynamic turbulence. The Lorentz equation for each particle of charge $q$ and mass $m$. The particle has a momentum $\mathbf{p}=\gamma m\mathbf{v}$ and a velocity $\mathbf{v}$ and propagates in an electromagnetic field $\mathbf{E}$ (no mean electric field), $\mathbf{B}=\delta \mathbf{B}+{\mathbf{B}}_0$:

$$\begin{array}{rl}\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}& =q(\mathbf{E}+\frac{\mathbf{v}}{c}\times \mathbf{B})\\ \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}& =\mathbf{v}\end{array}$$

Each particle is injected with a Lorentz factor ${\gamma }_0$. Physically, one can think of ${\gamma }_0$ as a measure of the relativity of the particle, i.e., for small ${\gamma }_0$ we will recover nonrelativistic equations, and for large ${\gamma }_0$ –- ultra-relativistic equations. ${\gamma }_0$ also defines the initial Larmor radius

$$r_{L0}={\gamma }_{0}m{c}^2/(e{B}_0)$$

where $B_0$ is background magnetic field strength. We also define the particle's synchrotron pulsation

$${\mathrm{\Omega }}_0=c/r_{L0}$$

This is measured in cyclotron frequency units, a gyration frequency measured in the particle's own frame. A particle with pitch angle cosine $\mu =\cos \theta =0$ will make a full orbit in the $B_0$ field in $2\pi$ time. After normalization, we have

$$\begin{array}{rl}\frac{\mathrm{d}{\mathbf{v}}^{\prime }}{\mathrm{d}{t}^{\prime }}& ={\gamma }^{\prime }{\mathbf{E}}^{\prime }+{\mathbf{v}}^{\prime }\times {\mathbf{B}}^{\prime }\\ \frac{\mathrm{d}{\mathbf{x}}^{\prime }}{\mathrm{d}{t}^{\prime }}& =\frac{r_{L0}}{L}{\mathbf{v}}^{\prime }\end{array}$$

where ${\gamma }^{\prime }=\gamma /{\gamma }_0$, ${\mathbf{v}}^{\prime }={\gamma }^{\prime }\mathbf{v}/c$, and $t^{\prime }=t/({\gamma }^{\prime }{r}_{L0}/c)$, ${\mathbf{E}}^{\prime }=\mathbf{E}/(B_0)$ is the normalized electric field, ${\mathbf{B}}^{\prime }=\mathbf{B}/B_0$ is the normalized magnetic field, and $x^{\prime }=x/L$. $L$ is the length scale we can choose to decide how many discrete point to have within one gyroradius. For instance, if $L=r_{L0}$, then 1 unit distance in the dimensionless system is 1 gyroradius for a particle with ${\gamma }_0$ under $B_0$; if $L=4r_{L0}$, then 1 unit distance in the dimensionless system is 4 gyroradii for a particle with ${\gamma }_0$ under $B_0$. The smaller $r_{L0}/L$ is, the more likely a particle will experience an inhomogeneous magnetic field during gyration, and the more likely it will get scattered. Note that ${\gamma }^{\prime }$ is also a function of $\mathbf{v}$:

$${\gamma }^{\prime }=\gamma /{\gamma }_0=\sqrt{\frac{1-v_0^2/c^2}{1-v^2/c^2}}$$

In practice, at least in the interstellar medium, the effect of the electric field over high-energy (multi TeV) cosmic rays can be neglected. Therefore, energy is conserved and we are interested in looking at the scattering and diffusion processes. ${\gamma }^{\prime }=1$ without considering radiative loss or re-acceleration.

Thus, the normalized equations can be further simplified:

$$\begin{array}{rl}\frac{\mathrm{d}{\mathbf{v}}^{\prime }}{\mathrm{d}{t}^{\prime }}& ={\mathbf{v}}^{\prime }\times {\mathbf{B}}^{\prime }\\ \frac{\mathrm{d}{\mathbf{x}}^{\prime }}{\mathrm{d}{t}^{\prime }}& =\frac{r_{L0}}{L}{\mathbf{v}}^{\prime }\end{array}$$

By taking $q=1,m=1,c=1,B_0=1$, the characteristic length and frequency scales are

$$\begin{array}{r}{r}_{L0}=\frac{{\gamma }_{0}m{c}^2}{e{B}_0}={\gamma }_0\\ {\mathrm{\Omega }}_0=\frac{e{B}_0}{m{c}^2}=1\end{array}$$

This looks good, but there is still an annoying factor $r_{L0}/L$ in the second equation. We can remove that by combining $L/r_{L0}$ with $\mathbf{x}$:

$$\frac{\mathrm{d}{\mathbf{x}}^{\prime }}{\mathrm{d}{t}^{\prime }}={\mathbf{v}}^{\prime }$$

It simply means that if the original domain length is 1, now it becomes $L/r_{L0}$.

A standard procedure is as follows:

1. Obtain the dimensionless MHD solution.

2. Normalize the magnetic field with its background mean magnitude, such that in the new field, $B_0=1$. This has a clear physical meaning that a particle with velocity 1 has a gyroradii of 1 and a gyroperiod of $2\pi$.

3. Manually choose the spatial extent to be $L/r_{L0}$. For simplicity, we set $r_{L0}=1$ and the MHD domain extent to be $[-L/2,L/2]$. If we have $nx$ discrete points along that direction, then the grid size is $dx=L/nx$. If $L=nx/4$, then $dx=1/4$ is a quarter of the gyroradius. In this way we can control how well we resolve the magnetic field for the gyromotion and diffusion process.

Now let's demonstrate this with trace_normalized!.

using TestParticle, OrdinaryDiffEqVerner, StaticArrays
using CairoMakie

# Number of cells for the field along each dimension
nx, ny, nz = 4, 6, 2
# Unit conversion factors for length
rL0 = 1.0
L = nx / 4
# Set length scales
x = range(-L/2-1e-2, L/2+1e-2, length = nx) # [rL0]
y = range(-L-1e-2, 1e-2, length = ny) # [rL0]
z = range(-10, 10, length = nz) # [rL0]

B = fill(0.0, 3, nx, ny, nz) # [B0]
B[3, :, :, :] .= 1.0
E(x) = SA[0.0, 0.0, 0.0] # [E₀]
# periodic bc = 2
param = prepare(x, y, z, E, B; species = User, bc = 2)

# Initial condition
stateinit = let
   x0 = [0.0, 0.0, 0.0] # initial position [l₀]
   u0 = [1.0, 0.0, 0.0] # initial velocity [v₀] -> r = 1 * rL0
   [x0..., u0...]
end
# Time span
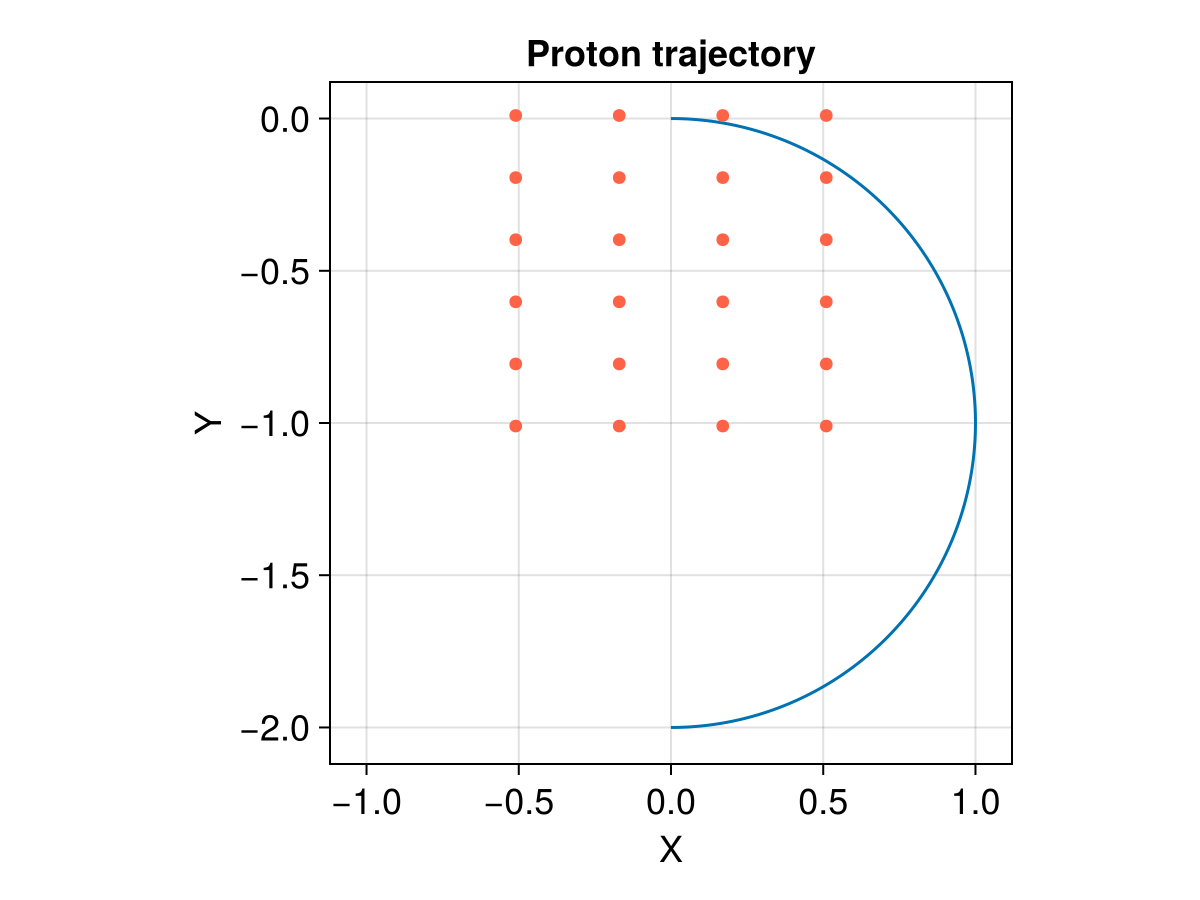
tspan = (0.0, π) # half gyroperiod

prob = ODEProblem(trace_normalized!, stateinit, tspan, param)
sol = solve(prob, Vern9())

### Visualization
f = Figure(fontsize = 18)
ax = Axis(f[1, 1],
   title = "Proton trajectory",
   xlabel = "X",
   ylabel = "Y",
   limits = (2*x[1]-0.1, 2*x[end]+0.1, 2*y[1]-0.1, 2*y[end]+0.1),
   aspect = DataAspect()
)

lines!(ax, sol, idxs = (1, 2))

xgrid = [i for i in x, _ in y]
ygrid = [j for _ in x, j in y]
scatter!(ax, xgrid[:], ygrid[:], color = :tomato)