Sampling from VDFs

This example demonstrates how to sample from various velocity distribution functions (VDFs) including Maxwellian, Bi-Maxwellian, Kappa, and Bi-Kappa distributions. We compare the sampled distributions with their theoretical probability density functions (PDFs).

using TestParticle
using SpecialFunctions: gamma
using Random
using StaticArrays
using Statistics
using CairoMakie

Random.seed!(1234)

Random.TaskLocalRNG()

Number of samples

N = 100_000;

Plotting configuration

theme = Theme(fontsize = 18)
set_theme!(theme)

1. Maxwellian Distribution

1D projection:

$$v\propto \exp (-\frac{v^2}{v_{th}^2})$$

# Parameters
u0 = [0.0, 0.0, 0.0]
p = 1.0 # Thermal pressure
n = 1.0 # Number density
m = 1.0 # Mass

# Construct distribution
vdf = Maxwellian(u0, p, n; m)
println(vdf)

# Sample
vs = rand(vdf, N)
vx = [v[1] for v in vs]

# Theoretical PDF
vth = vdf.vth
v_grid = range(-4vth, 4vth, length = 100)
pdf_maxwellian(v, vth) = exp(-v^2 / vth^2) / (sqrt(π) * vth)

# Visualization
f = Figure()
ax = Axis(f[1, 1], title = "Maxwellian", xlabel = "vx", ylabel = "PDF")
hist!(ax, vx, normalization = :pdf, bins = 50, label = "Sampled", color = (:blue, 0.5))
lines!(
   ax, v_grid, pdf_maxwellian.(v_grid, vth), label = "Theory", color = :red, linewidth = 2)
axislegend(ax)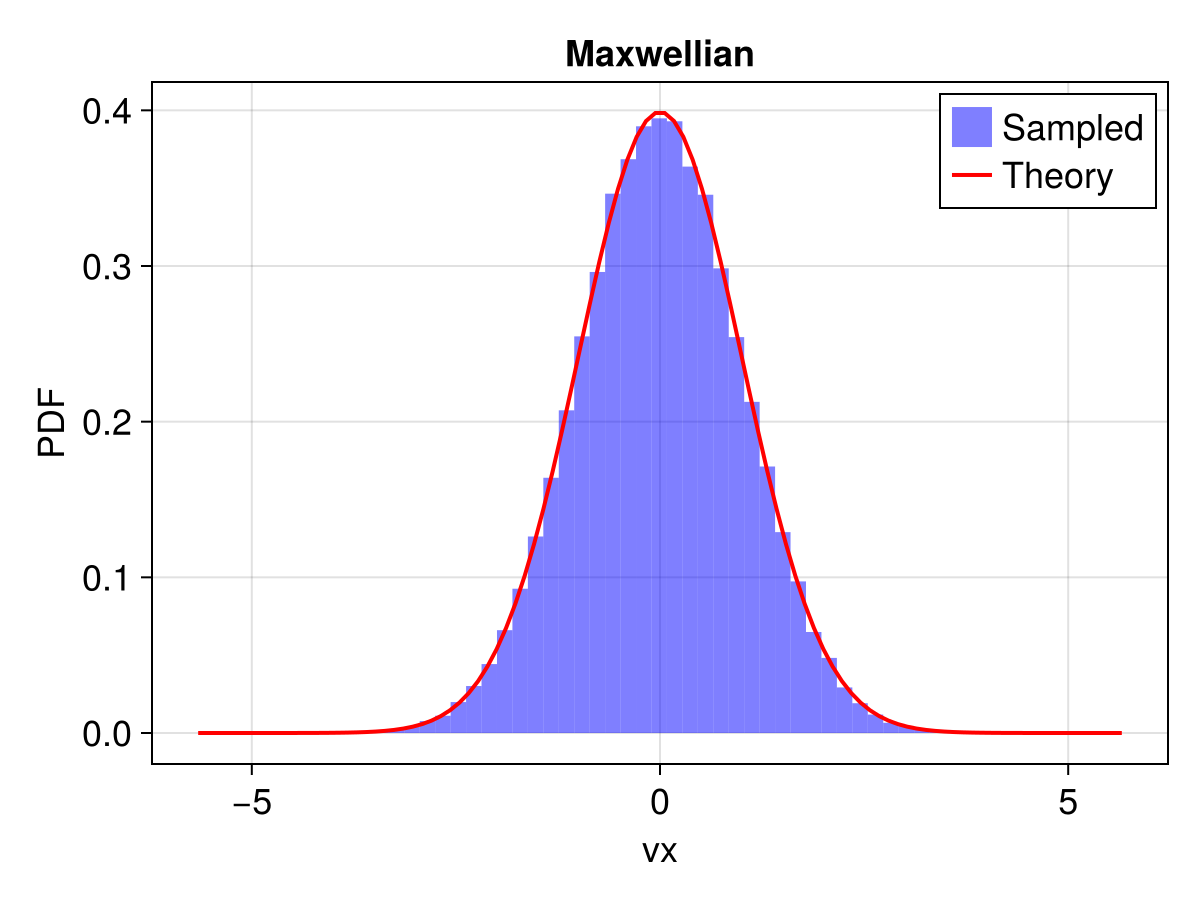

2. Bi-Maxwellian Distribution

$$v_{\parallel }\propto \exp (-\frac{v_{\parallel }^2}{v_{th,\parallel }^2})$$

2D magnitude:

$$v_{\perp }\propto \frac{v_{\perp }}{v_{th,\perp }^2}\exp (-\frac{v_{\perp }^2}{v_{th,\perp }^2})$$

# Parameters
B = [0.0, 0.0, 1.0]
ppar = 2.0
pperp = 0.5

# Construct distribution
vdf_bi = BiMaxwellian(B, u0, ppar, pperp, n; m)
println(vdf_bi)

# Sample
vs = rand(vdf_bi, N)
vpar = [v[3] for v in vs] # Since B is along Z
vperp = [hypot(v[1], v[2]) for v in vs]

# Theoretical PDFs
vthpar = vdf_bi.vth_para
vthperp = vdf_bi.vth_perp
# Bi-Maxwellian Parallel is identical to the 1D Maxwellian
pdf_bi_par(v, vth) = pdf_maxwellian(v, vth)
# Bi-Maxwellian Perpendicular (2D Speed / Rayleigh)
pdf_bi_perp(v, vth) = (2v / vth^2) * exp(-v^2 / vth^2)

# Visualization
f = Figure(size = (800, 400))
ax1 = Axis(f[1, 1], title = "Bi-Maxwellian Parallel (Z)", xlabel = "v_par", ylabel = "PDF")
hist!(ax1, vpar, normalization = :pdf, bins = 50, label = "Sampled", color = (:blue, 0.5))
lines!(
   ax1, v_grid, pdf_bi_par.(v_grid, vthpar), label = "Theory", color = :red, linewidth = 2)

ax2 = Axis(
   f[1, 2], title = "Bi-Maxwellian Perpendicular", xlabel = "v_perp", ylabel = "PDF")
hist!(ax2, vperp, normalization = :pdf, bins = 50, label = "Sampled", color = (:blue, 0.5))
v_grid_perp = range(0, 4vthperp, length = 100)
lines!(ax2, v_grid_perp, pdf_bi_perp.(v_grid_perp, vthperp),
   label = "Theory", color = :red, linewidth = 2)
axislegend(ax2)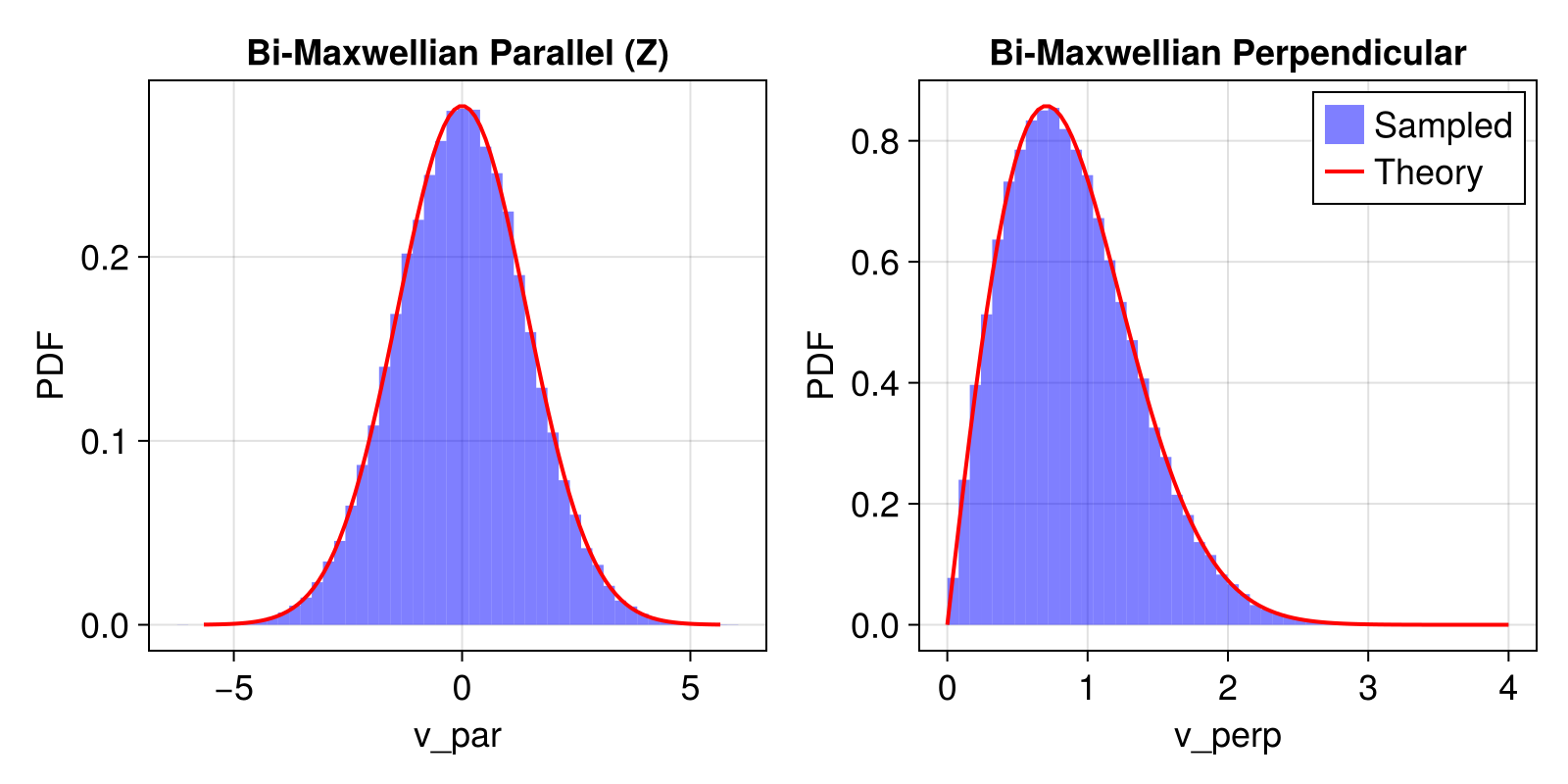

3. Kappa Distribution

1D projection

$$v\propto {(1+\frac{v^2}{(\kappa -1.5)v_{th}^2})}^{-\kappa -1}$$

# Parameters
kappa = 3.0

# Construct distribution
vdf_kappa = Kappa(u0, p, n, kappa; m)
println(vdf_kappa)

# Sample
vs = rand(vdf_kappa, N)
vx = [v[1] for v in vs]

# Theoretical PDF (1D projection of 3D Kappa)
# The 1D projection of a 3D Kappa distribution with parameter kappa is a 1D Kappa with parameter kappa.
# f(v) = A * (1 + v^2 / ((kappa - 1.5) * vth^2))^(-kappa)
# Normalization constant A = Gamma(kappa) / (sqrt(pi) * vth * sqrt(kappa - 1.5) * Gamma(kappa - 0.5))
function pdf_kappa(v, vth, k)
   theta2 = (k - 1.5) * vth^2
   A = gamma(k) / (sqrt(π * theta2) * gamma(k - 0.5))
   return A * (1 + v^2 / theta2)^(-k)
end

# Visualization
f = Figure()
ax = Axis(f[1, 1], title = "Kappa (kappa=3)", xlabel = "vx", ylabel = "PDF", yscale = log10)
hist!(ax, vx, normalization = :pdf, bins = 30, label = "Sampled", color = (:blue, 0.5))
lines!(ax, v_grid, pdf_kappa.(v_grid, vdf_kappa.vth, kappa),
   label = "Theory", color = :red, linewidth = 2)
axislegend(ax)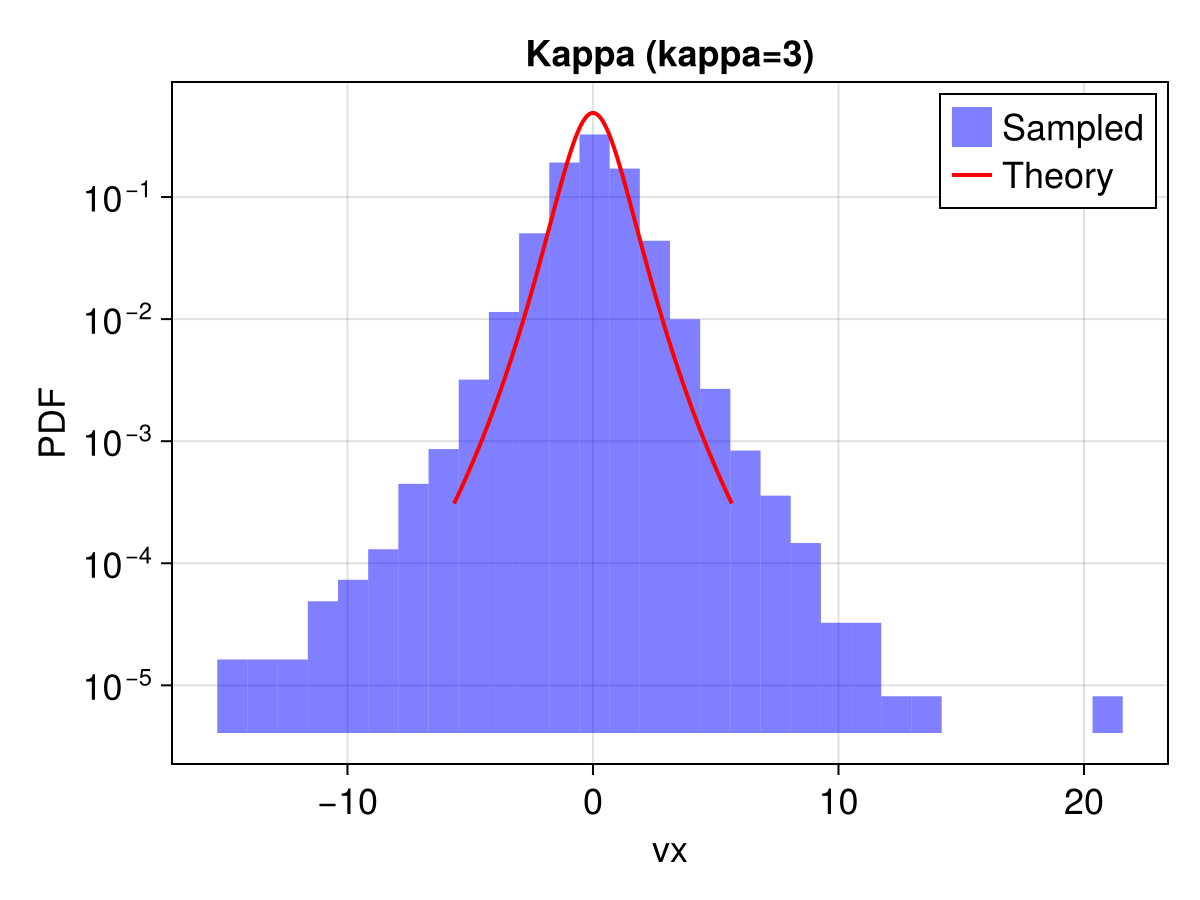

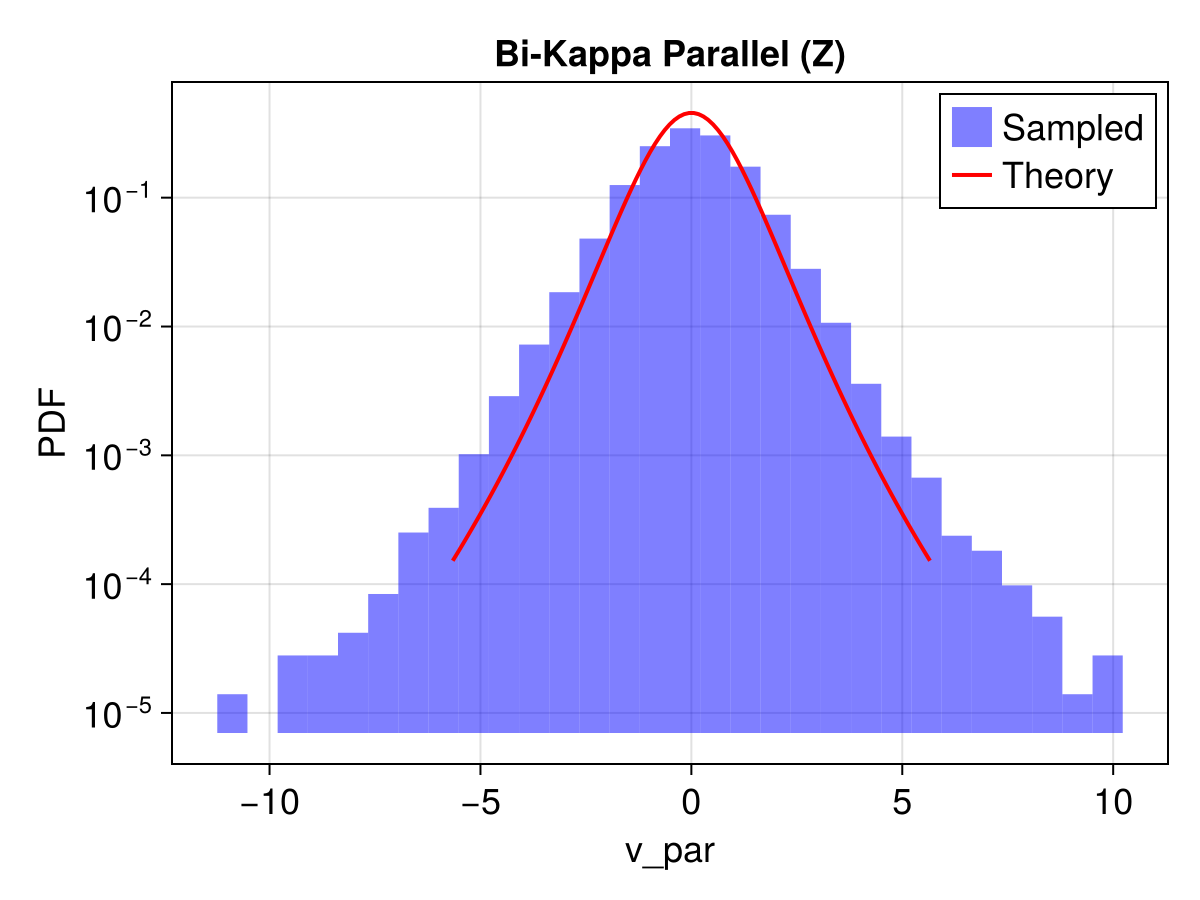
4. Bi-Kappa Distribution

Similar to Bi-Maxwellian but with power-law tails.

# Parameters
ppar = 1.0
pperp = 1.0
kappa = 4.0

# Construct distribution
vdf_bikappa = BiKappa(B, u0, ppar, pperp, n, kappa; m)
println(vdf_bikappa)

# Sample
vs = rand(vdf_bikappa, N)
vpar = [v[3] for v in vs]

# Theoretical PDF (1D projection)
# Similar form to isotropic Kappa 1D projection
pdf_bikappa_par(v, vth, k) = pdf_kappa(v, vth, k)

# Visualization
f = Figure()
ax = Axis(f[1, 1], title = "Bi-Kappa Parallel (Z)",
   xlabel = "v_par", ylabel = "PDF", yscale = log10)
hist!(ax, vpar, normalization = :pdf, bins = 30, label = "Sampled", color = (:blue, 0.5))
lines!(ax, v_grid, pdf_bikappa_par.(v_grid, vdf_bikappa.vth_para, kappa),
   label = "Theory", color = :red, linewidth = 2)
axislegend(ax)