Analytical Magnetosphere

This demo shows how to trace particles in a vacuum superposition of a dipolar magnetic field $B_{D}$ with a uniform background magnetic field $B_{IMF}$ . In this slightly modified dipole field, magnetic null points appear near 14 Earth's radii, and the particle orbits are also distorted from the idealized motions in Demo: magnetic dipole.

julia

using TestParticle, OrdinaryDiffEqVerner, StaticArrays
using TestParticle: getB_dipole, sph2cart, mᵢ, qᵢ, c, Rₑ, ZeroField
using FieldTracer
using CairoMakie

getB_superposition_constant(xu) = getB_dipole(xu) + SA[0.0, 0.0, -10.0e-9]

function getB_superposition_harris(xu)
    Bt = 0.01 * 4.0e-5 # [T], 1% of the dipole field at the equator
    δ = 0.1Rₑ # [m]
    Bx = Bt * tanh(-xu[3] / δ)
    return getB_dipole(xu) + SA[Bx, 0.0, 0.0]
end

"""
Boundary condition check.
"""
function isoutofdomain(u, p, t)
    rout = 18Rₑ
    if (u[1]^2 + u[2]^2 + u[3]^2) < (1.1Rₑ)^2 ||
            abs(u[1]) > rout || abs(u[2]) > rout || abs(u[3]) > rout
        return true
    else
        return false
    end
end

"""
Set initial conditions.
"""
function prob_func_13(prob, i, repeat)
    # initial particle energy
    Ek = 5.0e3 # [eV]
    # initial velocity, [m/s]
    v₀ = sph2cart(c * sqrt(1 - 1 / (1 + Ek * qᵢ / (mᵢ * c^2))^2), π / 4, 0.0)
    # initial position, [m]
    r₀ = sph2cart(13 * Rₑ, π * i, π / 2)

    return prob = remake(prob; u0 = [r₀..., v₀...])
end

function prob_func_6(prob, i, repeat)
    # initial particle energy
    Ek = 4.0e3 # [eV]
    # initial velocity, [m/s]
    v₀ = sph2cart(c * sqrt(1 - 1 / (1 + Ek * qᵢ / (mᵢ * c^2))^2), π / 4, 0.0)
    # initial position, [m]
    r₀ = sph2cart(6 * Rₑ, π / 2, 2π * i)

    return prob = remake(prob; u0 = [r₀..., v₀...])
end

# obtain field
param = prepare(ZeroField(), getB_superposition_constant)
stateinit = zeros(6) # particle position and velocity to be modified
tspan = (0.0, 2000.0)
trajectories = 2

prob = ODEProblem(trace!, stateinit, tspan, param)
ensemble_prob = EnsembleProblem(prob; prob_func = prob_func_13, safetycopy = false)

# See https://docs.sciml.ai/DiffEqDocs/stable/basics/common_solver_opts/
# for the solver options
callback = DiscreteCallback(isoutofdomain, terminate!)
sols = solve(
    ensemble_prob, Vern9(), EnsembleSerial(); reltol = 1.0e-5,
    trajectories, callback, dense = true, save_on = true
)

### Visualization

f = Figure(fontsize = 18)
ax = Axis3(
    f[1, 1],
    title = "5 keV Protons in a vacuum superposition magnetosphere",
    xlabel = "x [Re]",
    ylabel = "y [Re]",
    zlabel = "z [Re]",
    aspect = :data,
    limits = (-14, 14, -14, 14, -5, 5)
)

invRE = 1 / Rₑ

for (i, sol) in enumerate(sols)
    x = sol[1, :] .* invRE
    y = sol[2, :] .* invRE
    z = sol[3, :] .* invRE
    lines!(ax, x, y, z, color = Makie.wong_colors()[i])
end

# Field lines
function get_numerical_field(x, y, z, model)
    bx = zeros(length(x), length(y), length(z))
    by = similar(bx)
    bz = similar(bx)

    for i in CartesianIndices(bx)
        pos = [x[i[1]], y[i[2]], z[i[3]]]
        bx[i], by[i], bz[i] = model(pos)
    end

    return bx, by, bz
end

function trace_field!(
        ax, x, y, z, unitscale, model = getB_superposition_constant;
        rmin = 8Rₑ, rmax = 16Rₑ, nr = 8, nϕ = 4
    )
    bx, by, bz = get_numerical_field(x, y, z, model)

    zs = 0.0
    dϕ = 2π / nϕ
    for r in range(rmin, rmax, length = nr), ϕ in range(0, 2π - dϕ, length = nϕ)

        xs = r * cos(ϕ)
        ys = r * sin(ϕ)

        x1, y1,
            z1 = FieldTracer.trace(bx, by, bz, xs, ys, zs, x, y, z; ds = 0.1, maxstep = 10000)

        lines!(ax, x1 .* unitscale, y1 .* unitscale, z1 .* unitscale, color = :gray)
    end
    return
end

x = range(-18Rₑ, 18Rₑ, length = 50)
y = range(-18Rₑ, 18Rₑ, length = 50)
z = range(-18Rₑ, 18Rₑ, length = 50)

trace_field!(ax, x, y, z, invRE)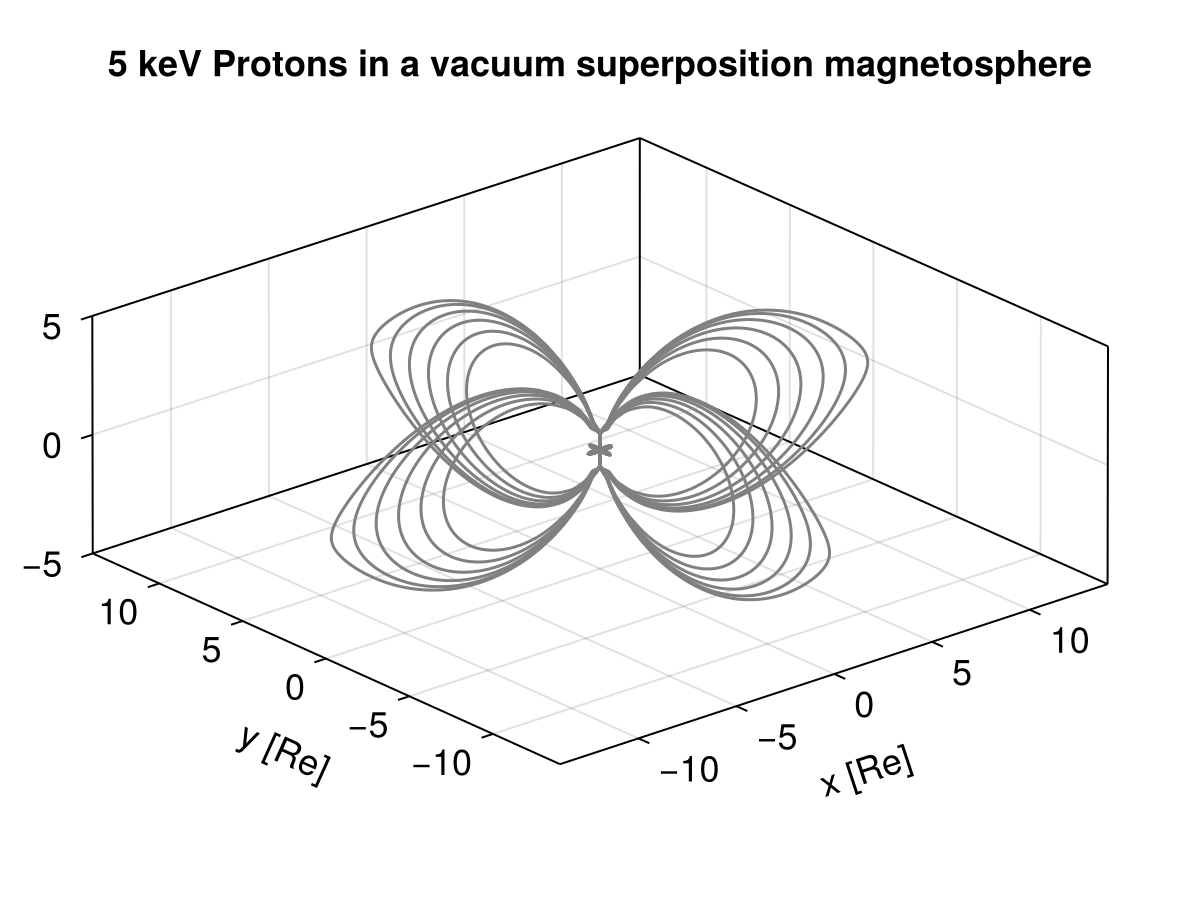

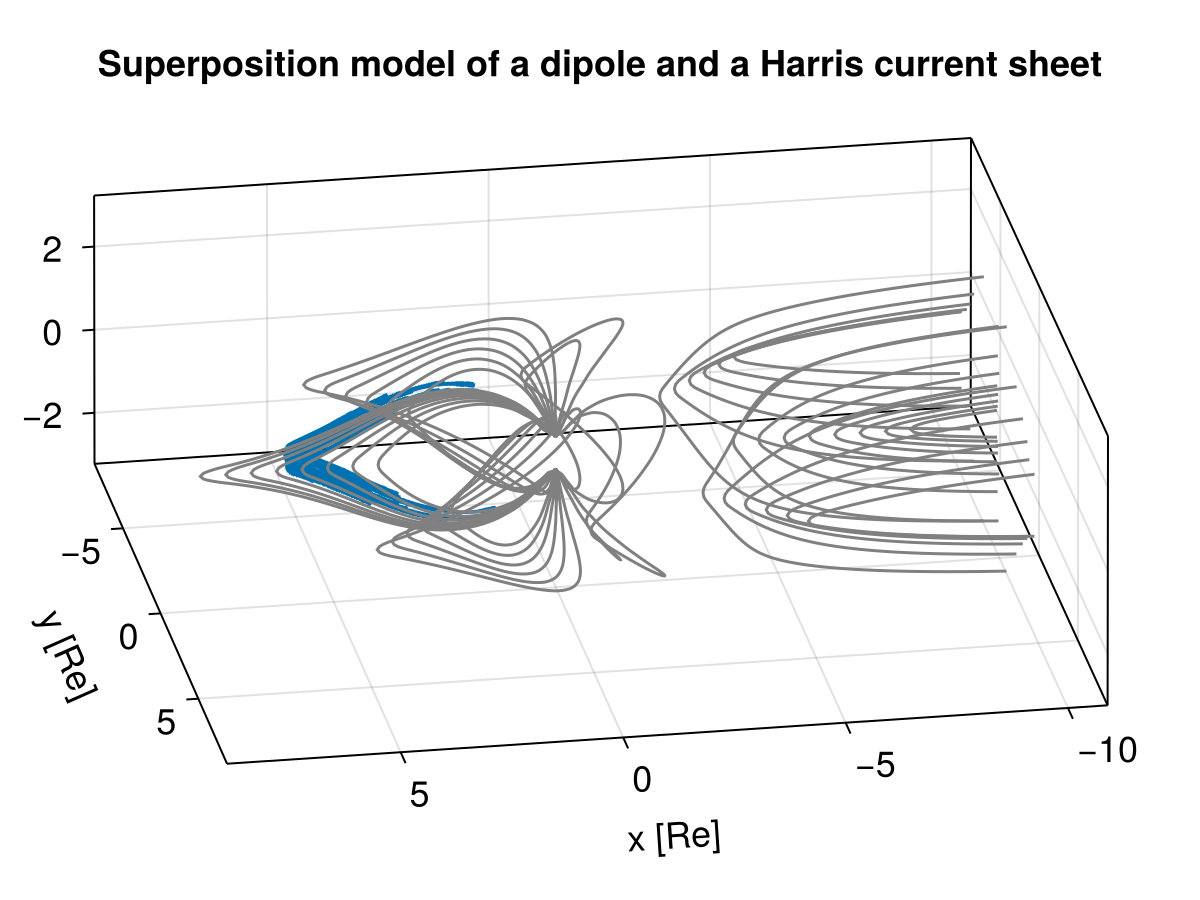
We now look at another superposition model of a dipole and a Harris current sheet.

julia

param = prepare(ZeroField(), getB_superposition_harris)
stateinit = zeros(6) # particle position and velocity to be modified
tspan = (0.0, 8000.0)
trajectories = 1

prob = ODEProblem(trace!, stateinit, tspan, param)
ensemble_prob = EnsembleProblem(prob; prob_func = prob_func_6, safetycopy = false)

callback = DiscreteCallback(isoutofdomain, terminate!)
sols = solve(
    ensemble_prob, Vern9(), EnsembleSerial(); reltol = 1.0e-5,
    trajectories, callback, dense = true, save_on = true
)

x = range(-10Rₑ, 10Rₑ, length = 50)
y = range(-5Rₑ, 5Rₑ, length = 20)
z = range(-10Rₑ, 10Rₑ, length = 50)

f = Figure(fontsize = 18)
ax = Axis3(
    f[1, 1],
    title = "Superposition model of a dipole and a Harris current sheet",
    xlabel = "x [Re]",
    ylabel = "y [Re]",
    zlabel = "z [Re]",
    aspect = :data,
    azimuth = 1.4
)

for (i, sol) in enumerate(sols)
    x = sol[1, :] .* invRE
    y = sol[2, :] .* invRE
    z = sol[3, :] .* invRE
    lines!(ax, x, y, z, color = Makie.wong_colors()[i])
end

trace_field!(ax, x, y, z, invRE, getB_superposition_harris; rmin = 4Rₑ, rmax = 8Rₑ, nϕ = 8)

Analytical Magnetosphere ​

Analytical Magnetosphere