Spherical Coordinates

This example demonstrates a single proton motion under a uniform B field defined in spherical coordinates following the same values in Demo: Helix motion. The E field is set to zero.

import TestParticle as TP
using OrdinaryDiffEq, StaticArrays
using CairoMakie

# Define the magnetic field in spherical coordinates
r = logrange(0.1, 10.0, length = 4)
θ = range(0, π, length = 8)
ϕ = range(0, 2π, length = 8)

B₀ = 1e-8 # [nT]
B = zeros(3, length(r), length(θ), length(ϕ))

for (iθ, θ_val) in enumerate(θ)
   sinθ, cosθ = sincos(θ_val)
   B[1, :, iθ, :] .= B₀ * cosθ
   B[2, :, iθ, :] .= -B₀ * sinθ
end

In TestParticle.jl v0.15, we introduced two new grid geometries: Spherical() and SphericalNonUniformR(). Spherical() assumes uniform range (r,θ,ϕ) coordinates, whereas SphericalNonUniformR() accepts non-uniform coordinates.

zero_E = TP.ZeroField()

# Initial condition
stateinit = let x0 = [1.0, 0.0, 0.0], v0 = [0.0, 1.0, 0.1]
   [x0..., v0...]
end
# Time span
tspan = (0, 18)

param = TP.prepare(
   r, θ, ϕ, zero_E, B; species = TP.Proton, gridtype = TP.SphericalNonUniformR())
prob = ODEProblem(TP.trace!, stateinit, tspan, param)
sol = solve(prob, Vern9())

# Visualization
f = Figure(fontsize = 18)
ax = Axis3(f[1, 1],
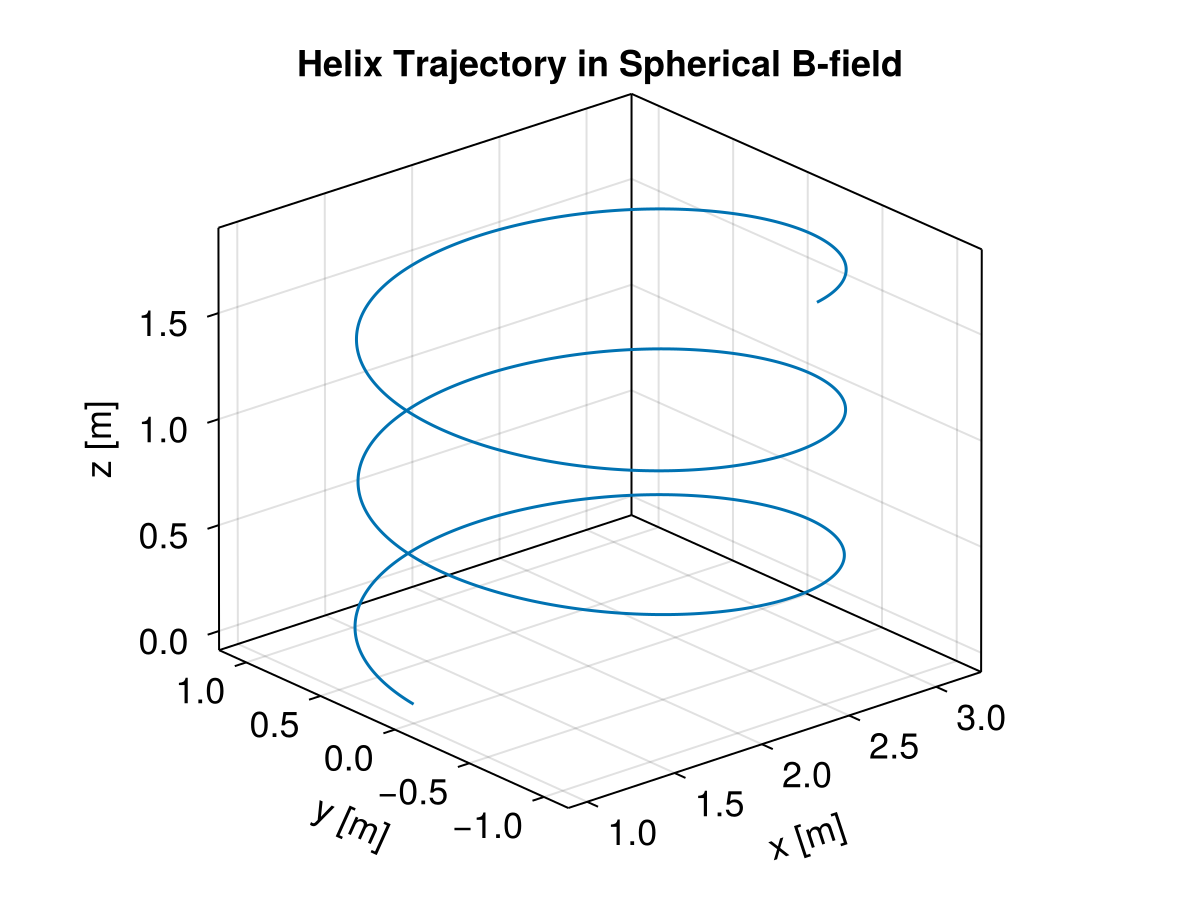
   title = "Helix Trajectory in Spherical B-field",
   xlabel = "x [m]",
   ylabel = "y [m]",
   zlabel = "z [m]",
   aspect = :data
)

plot!(ax, sol, idxs = (1, 2, 3))