Ensemble Tracing

This example demonstrates how to trace multiple particles efficiently using the EnsembleProblem interface from DifferentialEquations.jl. We cover three use cases:

Basic ensemble tracing with varying initial conditions.
Sampling initial velocities from a Maxwellian distribution.
Customizing output to save specific quantities (e.g., field values along trajectories).
Using the native Boris pusher for ensemble problems.

julia

using TestParticle
import TestParticle as TP
using VelocityDistributionFunctions
using OrdinaryDiffEqVerner
using StaticArrays
using Statistics
using LinearAlgebra
using Random
using CairoMakie

1. Basic Ensemble Tracing

In this section, we trace multiple electrons in a simple analytic EM field. We use prob_func to define unique initial conditions for each particle.

julia

B_analytic(x) = SA[0, 0, 1.0e-11]
E_analytic(x) = SA[0, 0, 1.0e-13]

# Initial state
x0 = [0.0, 0.0, 0.0] # initial position, [m]
u0 = [1.0, 0.0, 0.0] # initial velocity, [m/s]
stateinit = [x0..., u0...]

param = prepare(E_analytic, B_analytic, species = Electron)
tspan = (0.0, 10.0)

# Define the problem for a single particle
prob = ODEProblem(trace!, stateinit, tspan, param)

# Define prob_func to vary the initial x-velocity based on the particle index
prob_func_basic(prob, i, repeat) = remake(prob, u0 = [prob.u0[1:3]..., i / 3, 0.0, 0.0])

trajectories = 3
ensemble_prob = EnsembleProblem(prob; prob_func = prob_func_basic, safetycopy = false)
sols = solve(ensemble_prob, Vern7(), EnsembleThreads(); trajectories)

# Visualization
f = Figure(fontsize = 18)
ax = Axis3(
    f[1, 1], title = "Basic Ensemble", xlabel = "X",
    ylabel = "Y", zlabel = "Z", aspect = :data
)

for i in eachindex(sols)
    lines!(ax, sols[i], idxs = (1, 2, 3), label = "traj $i", color = Makie.wong_colors()[i])
end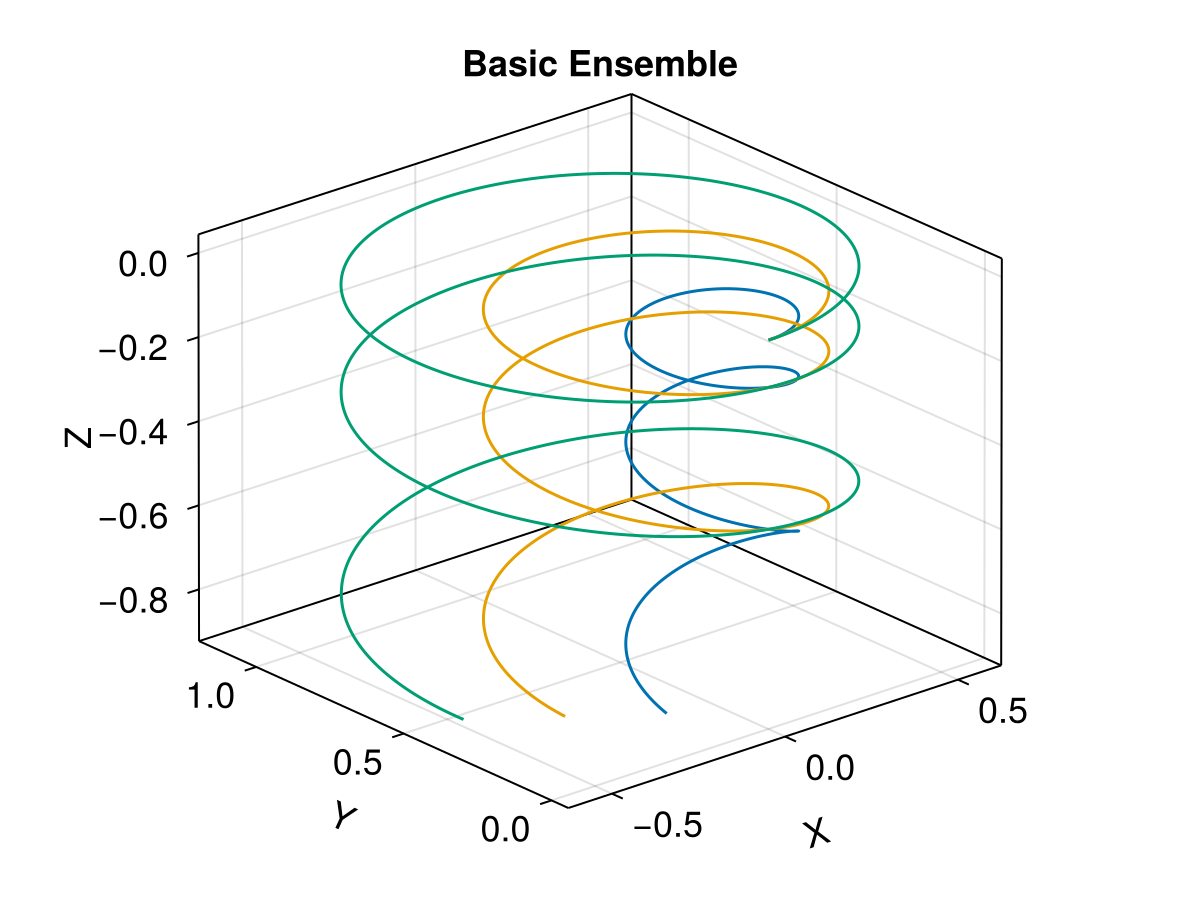

2. Sampling from a Distribution

Often we want to sample particle initial velocities from a distribution, such as a Maxwellian. Here we demonstrate how to do this using Maxwellian from TestParticle.jl.

julia

Random.seed!(1234)

# Define a new prob_func that samples from a Maxwellian
function prob_func_maxwellian(prob, i, repeat)
    # Sample from a Maxwellian with bulk speed 0 and thermal speed 1.0
    vdf = TP.Maxwellian([0.0, 0.0, 0.0], 1.0)
    v = rand(vdf)
    return remake(prob; u0 = [prob.u0[1:3]..., v...])
end

trajectories_dist = 10
ensemble_prob_dist = EnsembleProblem(prob; prob_func = prob_func_maxwellian, safetycopy = false)
sols_dist = solve(ensemble_prob_dist, Vern7(), EnsembleThreads(); trajectories = trajectories_dist)

# Visualization
f = Figure(fontsize = 18)
ax = Axis3(
    f[1, 1], title = "Maxwellian Sampling", xlabel = "X",
    ylabel = "Y", zlabel = "Z", aspect = :data
)

for i in eachindex(sols_dist)
    lines!(
        ax, sols_dist[i], idxs = (1, 2, 3), label = "$i",
        color = Makie.wong_colors()[mod1(i, 7)]
    )
end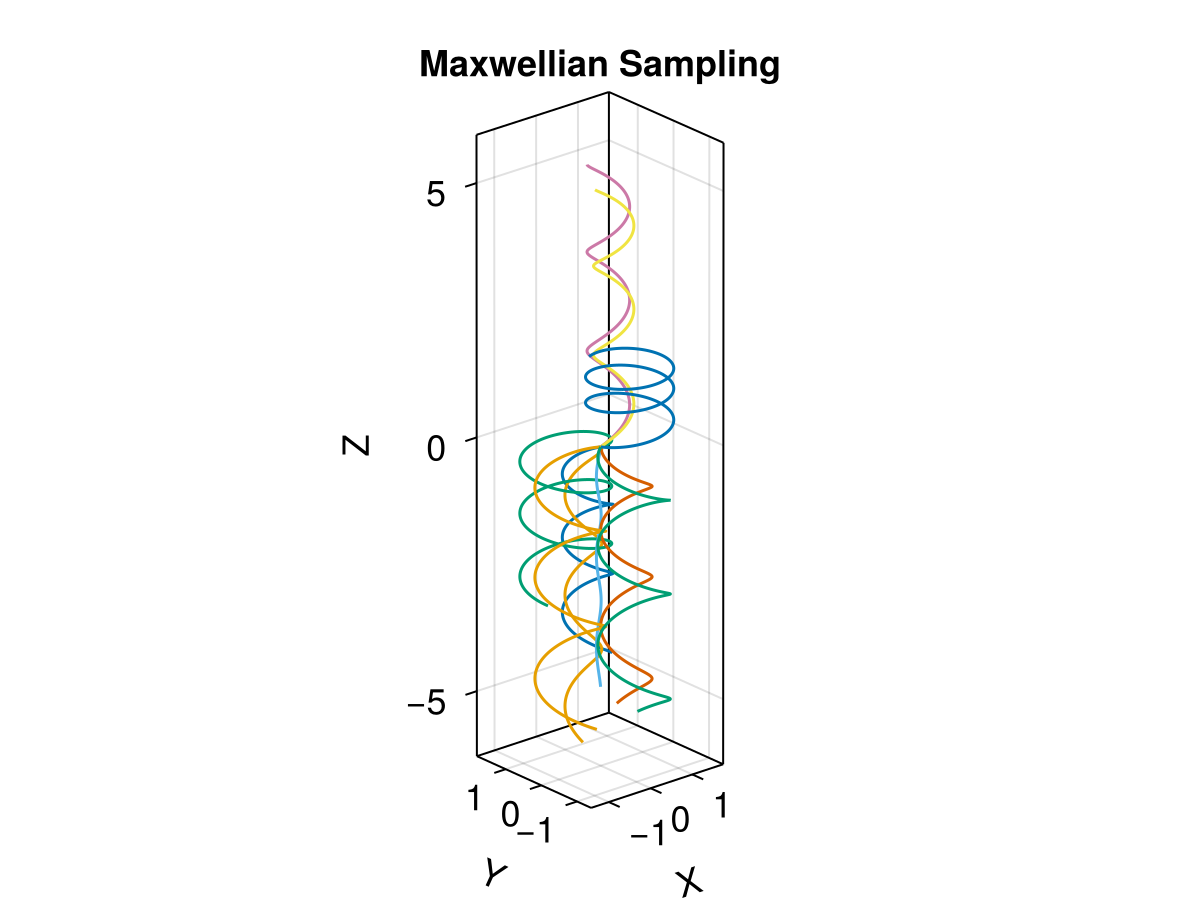

3. Custom Output (Reducing Memory Usage)

For large ensembles or long simulations, saving the full trajectory can be memory-intensive. The output_func argument allows us to save only what we need. Here, we save the magnetic field and the cosine of the pitch angle ( $μ$ ) along the trajectory.

We use a numerical field for this example to demonstrate a more complex setup. See Demo: Dimensionless Units for details on unit conversion.

julia

# Generate a numerical magnetic field
nx, ny, nz = 4, 6, 8
x_grid = range(0, 1, length = nx)
y_grid = range(0, 1, length = ny)
z_grid = range(0, 1, length = nz)
B_num = Array{Float32, 4}(undef, 3, nx, ny, nz)
B_num[1, :, :, :] .= 0.0
B_num[2, :, :, :] .= 0.0
B_num[3, :, :, :] .= 2.0

# Compute reference values
B₀ = get_mean_magnitude(B_num)
U₀ = 1.0
l₀ = 2 * nx
E₀ = U₀ * B₀

# Normalize units
x_norm = x_grid ./ l₀
y_norm = y_grid ./ l₀
z_norm = z_grid ./ l₀
B_norm = B_num ./ B₀
E_func(x) = SA[0.0, 0.0, 0.0] # E is zero

# Prepare parameters
# bc=2 uses periodic boundary conditions
param_custom = prepare(x_norm, y_norm, z_norm, E_func, B_norm; m = 1, q = 1, bc = 2)

# Initial condition
stateinit_custom = [0.0, 0.0, 0.0, 1.0, 0.0, 0.0]
tspan_custom = (0.0, 2π)

prob_custom = ODEProblem(trace_normalized!, stateinit_custom, tspan_custom, param_custom)

# Define prob_func to initialize particles with different pitch angles
function prob_func_custom(prob, i, repeat)
    B0 = TP.get_BField(prob)(prob.u0)
    B0 = normalize(B0)

    Bperp1 = normalize(SA[0.0, -B0[3], B0[2]])
    Bperp2 = normalize(B0 × Bperp1)

    ϕ = 2π * rand()
    θ = acos(0.5) # constant pitch angle for demonstration
    sinϕ, cosϕ = sincos(ϕ)

    u = @. (B0 * cos(θ) + Bperp1 * (sin(θ) * cosϕ) + Bperp2 * (sin(θ) * sinϕ)) * U₀
    return remake(prob; u0 = [prob.u0[1:3]..., u...])
end

# Define output_func to save specific data
function output_func_custom(sol, i)
    getB = TP.get_BField(sol)
    b = getB.(sol.u)

    # Calculate cosine of pitch angle
    μ = [
        @views (b[j] ⋅ sol[4:6, j]) / (norm(b[j]) * norm(sol[4:6, j]))
            for j in eachindex(sol)
    ]

    # Return: (trajectory, B-field, pitch-angle-cosine), rerun_flag
    return (sol.u, b, μ), false
end

trajectories_custom = 2
saveat = tspan_custom[2] / 40

ensemble_prob_custom = EnsembleProblem(
    prob_custom;
    prob_func = prob_func_custom,
    output_func = output_func_custom,
    safetycopy = false
)

sols_custom = solve(
    ensemble_prob_custom, Vern9(), EnsembleThreads();
    trajectories = trajectories_custom,
    saveat = saveat
)

# Visualization
f = Figure(fontsize = 18)
ax = Axis3(
    f[1, 1], title = "Custom Output Trajectories",
    xlabel = "X", ylabel = "Y", zlabel = "Z", aspect = :data
)

for i in eachindex(sols_custom)
    # sols_custom[i][1] contains the trajectory (u)
    xp = [s[1] for s in sols_custom[i][1]]
    yp = [s[2] for s in sols_custom[i][1]]
    zp = [s[3] for s in sols_custom[i][1]]
    lines!(ax, xp, yp, zp, label = "$i")
end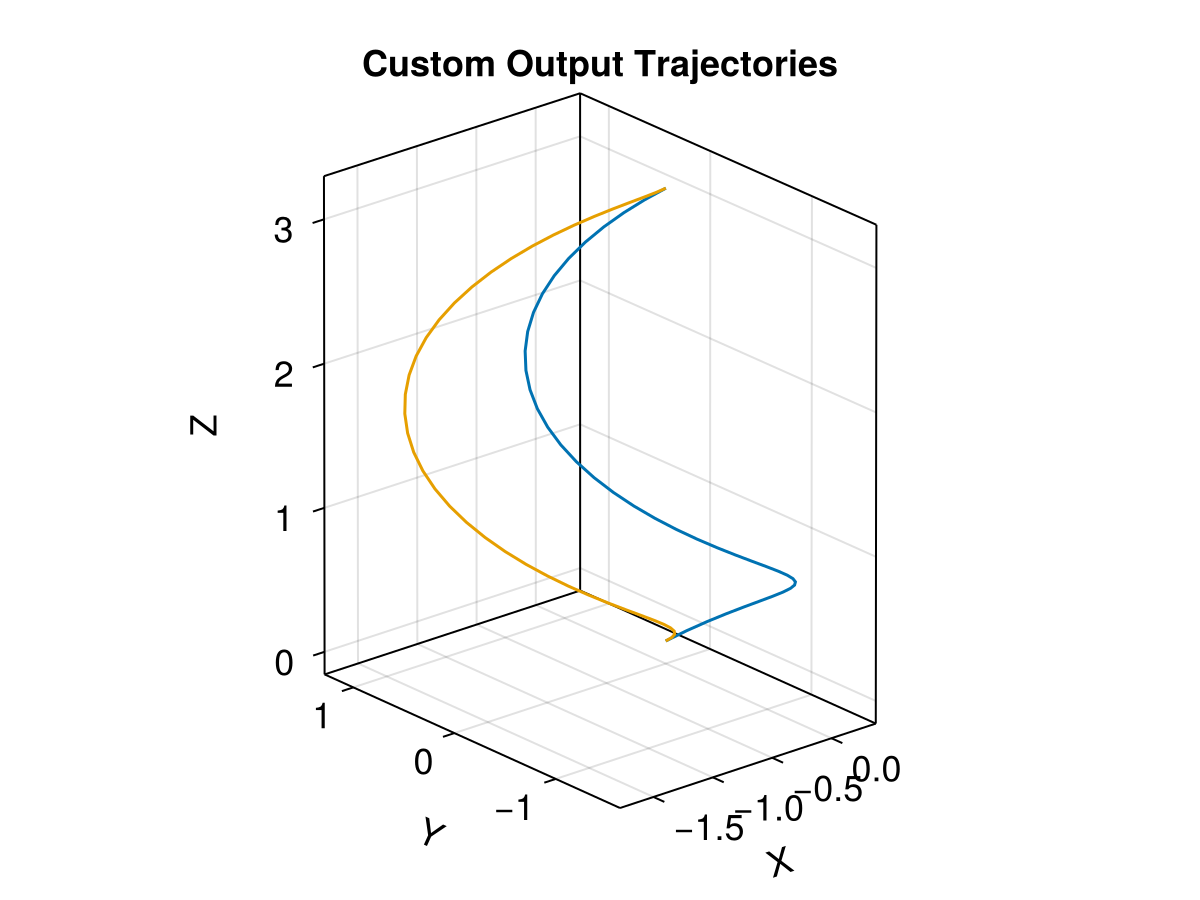

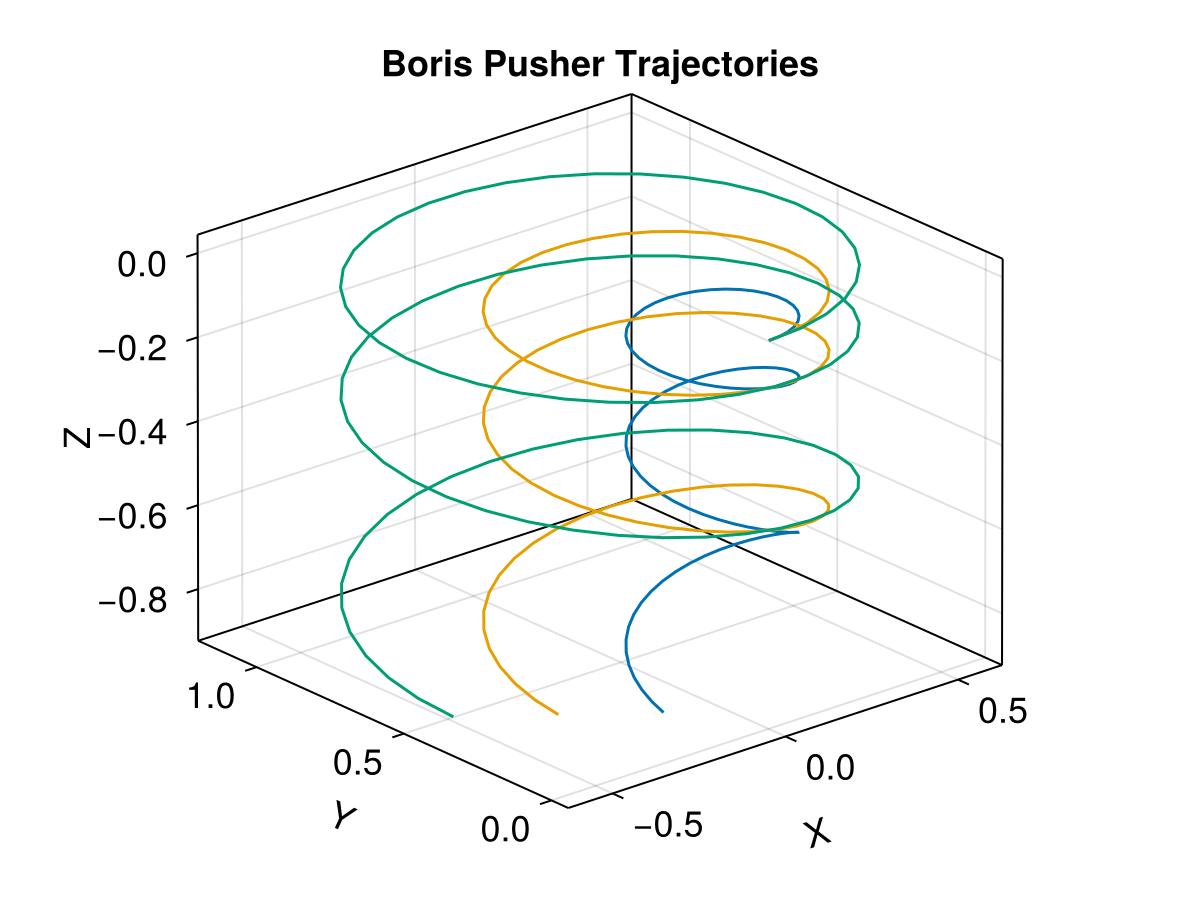
4. Native Boris Pusher

We can also solve the ensemble problem with the native Boris pusher. Note that the Boris pusher requires additional parameters: a fixed timestep, and an output save interval.

julia

dt = 0.1
savestepinterval = 1

# Reuse the basic problem parameters
prob_boris = TraceProblem(stateinit, tspan, param; prob_func = prob_func_basic)
trajs_boris = TestParticle.solve(prob_boris; dt, trajectories = 3, savestepinterval)

# Visualization
f = Figure(fontsize = 18)
ax = Axis3(
    f[1, 1], title = "Boris Pusher Trajectories",
    xlabel = "X", ylabel = "Y", zlabel = "Z", aspect = :data
)

for i in eachindex(trajs_boris)
    lines!(
        ax, trajs_boris[i]; idxs = (1, 2, 3), label = "$i", color = Makie.wong_colors()[i]
    )
end

Ensemble Tracing ​

1. Basic Ensemble Tracing ​

2. Sampling from a Distribution ​

3. Custom Output (Reducing Memory Usage) ​

4. Native Boris Pusher ​

Ensemble Tracing

1. Basic Ensemble Tracing

2. Sampling from a Distribution

3. Custom Output (Reducing Memory Usage)

4. Native Boris Pusher