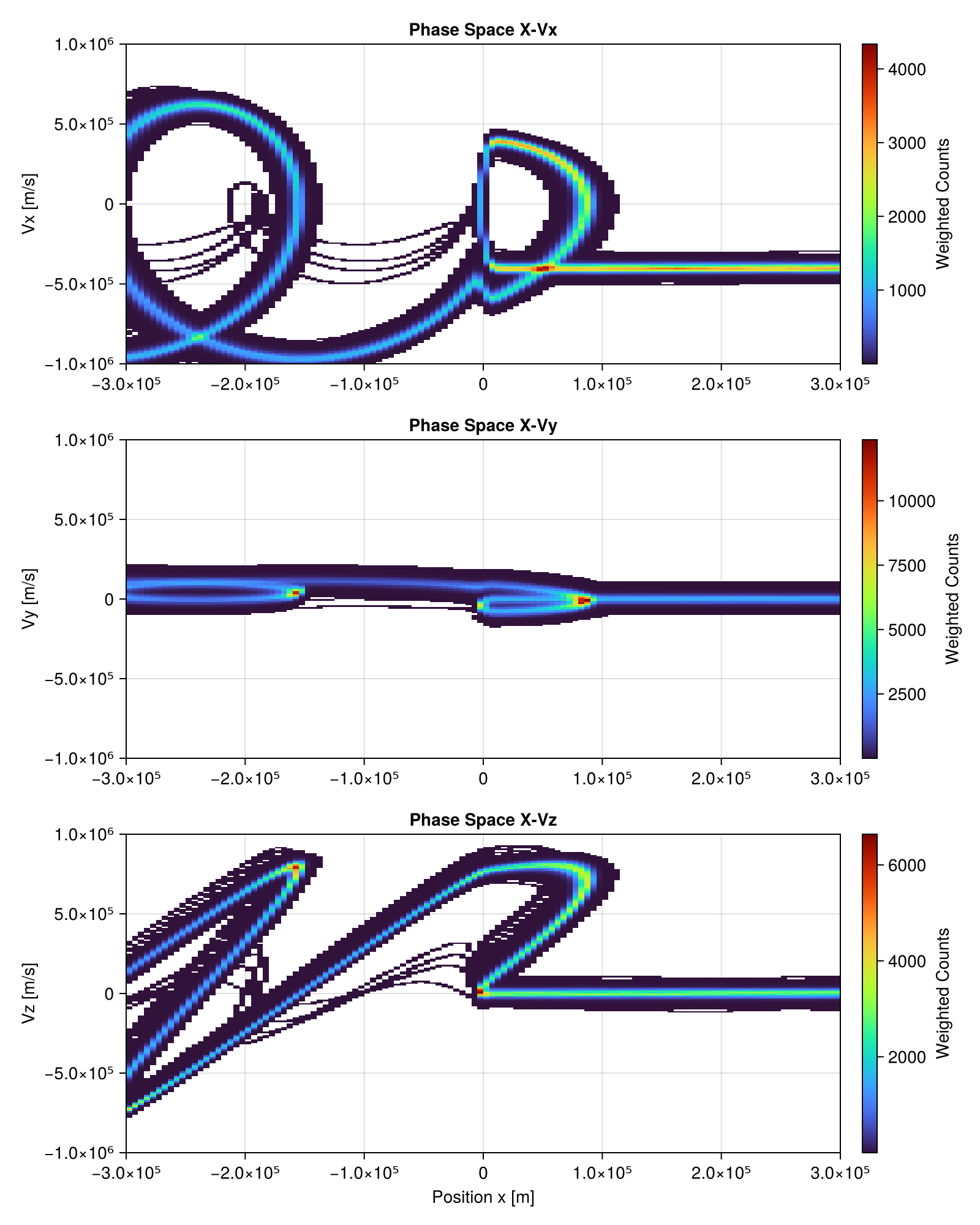
Shock Phase Space

This example demonstrates how to trace ions across a collisionless shock and analyze their phase space distribution, following the demo from IRF-matlab. We utilize Liouville's theorem (phase space density conservation) and backward/forward tracing to reconstruct the distribution function. In this specific example, we trace particles forward from a Maxwellian distribution upstream to seeing their evolution downstream.

using TestParticle
import TestParticle as TP
using StaticArrays
using OrdinaryDiffEqVerner
using Random
using FHist
using CairoMakie

Random.seed!(42);

Physics Constants & Parameters

We use analytical profiles to represent the shock transition.

const m_p = TP.mᵢ
const e = TP.qᵢ
const μ₀ = TP.μ₀

const Tiw = 12.0 # eV
const Tio = 3.0  # eV
const vithw = sqrt(2 * e * Tiw / m_p) # ~47.9 km/s
const vitho = sqrt(2 * e * Tio / m_p) # ~24.0 km/s

const Vsw = -400.0e3 # m/s
const nsw = 5.0e6  # m^-3
const P0_val = 0.08e-9 # Pa
const l_shock = 5.0e3 # m

# Shock Parameters
const n0_p = 3.0e6 # m^-3
const n1_p = 8.0e6 # m^-3

# Magnetic Field Parameters
const theta = 45.0
const Bmagnitude = 30.0 # nT

function get_B0_B1(theta, B_mag)
    theta_rad = deg2rad(theta)
    Bup_x = B_mag * cos(theta_rad)
    Bup_y = B_mag * sin(theta_rad)
    Bup_mag = B_mag

    Bdown_x = Bup_x
    Bdown_y = 3 * Bup_y
    Bdown_mag = sqrt(Bdown_x^2 + Bdown_y^2)

    B0 = 0.5 * (Bdown_mag - Bup_mag)
    B1 = 0.5 * (Bup_mag + Bdown_mag)
    return B0, B1
end

B0_calc, B1_calc = get_B0_B1(theta, Bmagnitude)
const B0_val = B0_calc * 1.0e-9 # T
const B1_val = B1_calc * 1.0e-9 # T
const Bx_val = 5.0e-9; # T

Field Definitions

We define custom analytical functions for the electric and magnetic fields across the shock.

"""
Magnetic Field
"""
function get_B_shock(r)
    x = r[1]
    by = -B0_val * tanh(x / l_shock) + B1_val
    bx = Bx_val
    bz = 0.0
    return SVector{3}(bx, by, bz)
end

"""
Electric Field based on generalized Ohm's law, including the Hall term and Electron Pressure Gradient.
"""
function get_E_shock(r)
    x = r[1]
    tanh_v = tanh(x / l_shock)
    sech_v = sech(x / l_shock)
    # Ion density for Harris current sheet
    ni = -n0_p * tanh_v + n1_p

    # Jz from Ampere's Law
    jz = -B0_val * sech_v^2 / (μ₀ * l_shock)

    by = -B0_val * tanh_v + B1_val
    bx = Bx_val

    # Ohm's Law and momentum equation terms
    ex = -jz * by / (e * ni) + P0_val * sech_v^2 / (e * ni * l_shock)
    ey = jz * bx / (e * ni)
    ez = -Vsw * (B1_val - B0_val)

    return SVector{3}(ex, ey, ez)
end;

Simulation Setup

trajectories = 1000 # number of particles
tspan = (0.0, 50.0) # s
dt_interp = 1.0e-3 # s

# Prepare the Hamiltonian system
param = prepare(get_E_shock, get_B_shock; species = Proton)

# Generate random initial velocities (Maxwellian)
const vxi_rand = randn(trajectories) .* (vithw / sqrt(2))
const vyi_rand = randn(trajectories) .* (vithw / sqrt(2))
const vzi_rand = randn(trajectories) .* (vithw / sqrt(2))
viabs = @. sqrt(vxi_rand^2 + vyi_rand^2 + vzi_rand^2)
const vxi_init = vxi_rand .+ Vsw # Shift by solar wind speed

# Calculate weights (if needed for non-Maxwellian initialization logic)
const weight_factor = (vithw / vitho)^3
const exp_factor = (vitho^2 - vithw^2) / (vitho^2 * vithw^2)
weights = weight_factor .* exp.(viabs .^ 2 .* exp_factor)

# Initial Conditions (Upstream)
function prob_func(prob, i, repeat)
    x0_start = 300.0e3
    y0_start = 0.0
    z0_start = 0.0

    vx = vxi_init[i]
    vy = vyi_rand[i]
    vz = vzi_rand[i]
    u0 = [x0_start, y0_start, z0_start, vx, vy, vz]

    return remake(prob, u0 = u0)
end

u0_dummy = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
prob = TraceProblem(u0_dummy, tspan, param; prob_func)

println("Starting simulation with $trajectories particles...")
@time sols = TP.solve(prob; dt = dt_interp, savestepinterval = 1, trajectories);
println("Simulation complete.")

Starting simulation with 1000 particles...
  8.376980 seconds (984.98 k allocations: 2.656 GiB, 31.62% gc time, 2.65% compilation time)
Simulation complete.

Analysis and Plotting

We bin the particle trajectories into phase space histograms.

function bin_results(sols, weights)
    println("Binning results...")
    xrange = [-300, 300] .* 1.0e3
    dxx = 5.0e3
    vrange = [-1000, 1000] .* 1.0e3
    dv = 10.0e3

    x_edges = xrange[1]:dxx:xrange[2]
    v_edges = vrange[1]:dv:vrange[2]

    h_x_vx = Hist2D(; binedges = (x_edges, v_edges))
    h_x_vy = Hist2D(; binedges = (x_edges, v_edges))
    h_x_vz = Hist2D(; binedges = (x_edges, v_edges))

    # Binning loop
    for i in eachindex(sols)
        s = sols[i]
        w = weights[i]

        for state in s.u
            x = state[1]
            vx = state[4]
            vy = state[5]
            vz = state[6]

            push!(h_x_vx, x, vx, w)
            push!(h_x_vy, x, vy, w)
            push!(h_x_vz, x, vz, w)
        end
    end
    println("Binning complete.")

    return h_x_vx, h_x_vy, h_x_vz
end

h_x_vx, h_x_vy, h_x_vz = bin_results(sols, weights);

Binning results...
Binning complete.

Phase Space Plots

fig = Figure(size = (800, 1000))

ax1 = Axis(fig[1, 1], title = "Phase Space X-Vx", ylabel = "Vx [m/s]")
hm1 = heatmap!(ax1, h_x_vx, colormap = :turbo)
Colorbar(fig[1, 2], hm1, label = "Weighted Counts")

ax2 = Axis(fig[2, 1], title = "Phase Space X-Vy", ylabel = "Vy [m/s]")
hm2 = heatmap!(ax2, h_x_vy, colormap = :turbo)
Colorbar(fig[2, 2], hm2, label = "Weighted Counts")

ax3 = Axis(
    fig[3, 1], title = "Phase Space X-Vz", xlabel = "Position x [m]", ylabel = "Vz [m/s]"
)
hm3 = heatmap!(ax3, h_x_vz, colormap = :turbo)
Colorbar(fig[3, 2], hm3, label = "Weighted Counts")