3 Math
3.1 Vector Identities
Some useful vector identities are listed below: \[ \begin{aligned} \mathbf{A}\times(\mathbf{B}\times\mathbf{C}) &= \mathbf{B}(\mathbf{A}\cdot\mathbf{C}) + \mathbf{C}(\mathbf{A}\cdot\mathbf{B}) \\ (\mathbf{A}\times\mathbf{B})\times\mathbf{C} &= \mathbf{B}(\mathbf{A}\cdot\mathbf{C}) + \mathbf{A}(\mathbf{B}\cdot\mathbf{C}) \\ \nabla\times\nabla f &= 0 \\ \nabla\cdot(\nabla\times\mathbf{A}) &= 0 \\ \nabla\cdot(f\mathbf{A}) &= (\nabla f)\cdot\mathbf{A} + f\nabla\cdot\mathbf{A} \\ \nabla\times(f\mathbf{A}) &= (\nabla f)\times\mathbf{A} + f\nabla\times\mathbf{A} \\ \nabla\cdot(\mathbf{A}\times\mathbf{B}) &= \mathbf{B}\cdot(\nabla\times\mathbf{A}) - \mathbf{A}\cdot(\nabla\times\mathbf{B}) \\ \nabla(\mathbf{A}\cdot\mathbf{B}) &= (\mathbf{B}\cdot\nabla)\mathbf{A} + (\mathbf{A}\cdot\nabla)\mathbf{B} + \mathbf{B}\times(\nabla\times\mathbf{A}) + \mathbf{A}\times(\nabla\times\mathbf{B}) \\ \nabla\cdot(\mathbf{A}\mathbf{B}) &= (\mathbf{A}\cdot\nabla)\mathbf{B} + \mathbf{B}(\nabla\cdot\mathbf{A}) \\ \nabla\times(\mathbf{A}\times\mathbf{B}) &= (\mathbf{B}\cdot\nabla)\mathbf{A} - (\mathbf{A}\cdot\nabla)\mathbf{B} - \mathbf{B}(\nabla\cdot\mathbf{A}) + \mathbf{A}(\nabla\cdot\mathbf{B}) \\ \nabla\times(\nabla\times\mathbf{A}) &= \nabla(\nabla\cdot\mathbf{A}) - \nabla^2\mathbf{A} \end{aligned} \]
In most cases Einsten notation shall be used to derive all the identities: \[ y = \sum_{i=1}^3 c_i x^i = c_1 x^1 + c_2 x^2 + c_3 x^3 \]
is simplified by the convention to \[ y = c_i x^i \]
The upper indices are not exponents but are indices of coordinates, coefficients or basis vectors. That is, in this context \(x^2\) should be understood as the second component of \(x\) rather than the square of \(x\) (this can occasionally lead to ambiguity). The upper index position in \(x^i\) is because, typically, an index occurs once in an upper (superscript) and once in a lower (subscript) position in a term.
A basis gives such a form (via the dual basis), hence when working on \(\mathbf{R}^n\) with a Euclidean metric and a fixed orthonormal basis, one has the option to work with only subscripts. However, if one changes coordinates, the way that coefficients change depends on the variance of the object, and one cannot ignore the distinction. (See this wiki link.)
Commonly used identities: \[ \begin{aligned} \mathbf{A}\cdot\mathbf{B} &= A_i B_i \\ \mathbf{A}\times\mathbf{B} &= \epsilon_{ijk}A_j B_k \\ \nabla\cdot\mathbf{A} &= \partial_i A_i \\ \nabla\times\mathbf{A} &= \epsilon_{ijk}\partial_j A_k \\ \epsilon_{ijk}\epsilon_{imn} &= \delta_{jm}\delta_{kn} - \delta_{jn}\delta_{km} \end{aligned} \]
3.2 Differential of Line Segments
The differential of line segments in a fluid is: \[ \frac{\mathrm{d}\mathbf{l}}{\mathrm{d}t} = \mathbf{l}\cdot\nabla\mathbf{u} \tag{3.1}\]
Proof. Let the two line segments \(\mathbf{l}_1\) and \(\mathbf{l}_2\) be expressed as starting point vectors and end point vectors: \[ \begin{aligned} \mathbf{l}_1&=\mathbf{r}_2 -\mathbf{r}_1 \\ \mathbf{l}_2&=\mathbf{r}_2^\prime -\mathbf{r}_1^\prime \end{aligned} \]
After time \(\Delta t\), \(\mathbf{l}_1\rightarrow \mathbf{l}_2\), \[ \mathbf{l}_2=\mathbf{r}_2^\prime -\mathbf{r}_1^\prime=(\mathbf{r}_2 +\mathbf{v}(r_2)\Delta t)-(\mathbf{r}_1+\mathbf{v}(\mathbf{r}_1)\Delta t)=\mathbf{l}_1+(\mathbf{v}(\mathbf{r}_2)-\mathbf{v}(\mathbf{r}_1))\Delta t \]
The velocity difference can be written as \[ \mathbf{v}(x_2,y_2,z_2)-\mathbf{v}(x_1,y_1,z_1) = \frac{\partial\mathbf{v}}{\partial x}(x_2-x_1) +\frac{\partial\mathbf{v}}{\partial y}(y_2-y_1) +\frac{\partial\mathbf{v}}{\partial z}(z_2-z_1) =(\mathbf{l}\cdot\nabla)\mathbf{v} \]
So \[ \mathbf{l}_2=\mathbf{l}_1+\mathbf{l}\cdot\nabla\mathbf{v}\cdot\Delta t\Rightarrow \frac{\mathbf{l}_2-\mathbf{l}_1}{\Delta t}=\mathbf{l}\cdot\nabla\mathbf{v} \] □
3.3 Lagrangian vs Eulerian Descriptions
The Lagrangian operator \(\mathrm{d}/\mathrm{d}t\) is defined to be the convective derivative \[ \frac{\mathrm{d}}{\mathrm{d}t} = \frac{\partial}{\partial t} + \mathbf{u}\cdot\nabla \tag{3.2}\] which characterizes the temporal rate of change seen by an observer moving with the velocity \(\mathbf{u}\). An everyday example of the convective term would be the apparent temporal increase in density of automobiles seen by a motorcyclist who enters a traffic jam of stationary vehicles and is not impeded by the traffic jam.
The convective derivative is sometimes written as \(\mathrm{D}/\mathrm{D}t\), which is used to emphasize the fact that the this specific convective derivative is defined using the center-of-mass velocity. Note that \((\mathbf{u}\cdot\nabla)\) is a scalar differential operator.
3.4 Complex Analysis
In complex analysis, the following statements are equivalent:
- \(f(z)\) is an analytic function of \(z\) in some neighbourhood of \(z_0\).
- \(\oint_C f(z)dz=0\) for every closed contour \(C\) that lies in that neighbourhood of \(z_0\).
- \(df(z)/dz\) exists at \(z=z_0\).
- \(f(z)\) has a convergent Taylor expansion about \(z=z_0\).
- The \(n^{th}\) derivative \(\mathrm{d}^nf(z)/dz^n\) exists at \(z=z_0\) for all \(n\).
- The Cauchy-Riemann condition is satisfied at \(z=z_0\). Take \(u\) and \(v\) to be the real and imaginary parts respectively of a complex-valued function of a single complex variable \(z = x + iy\), \(f(x + iy) = u(x,y) + iv(x,y)\).
\[ \begin{aligned} \frac{\partial u}{\partial x}&=\frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y}&=-\frac{\partial v}{\partial x} \end{aligned} \]
An idea of analytic continuation is introduced here. In practice, an analytic function is usually defined by means of some mathematical expression — such as a polynomial, an infinite series, or an integral. Ordinarily, there is some region within which the expression is meaningful and does yield an analytic function. Outside this region, the expression may cease to be meaningful, and the question then arises as to whether or not there is any way of extending the definition of the function so that this “extended” function is analytic over a larger region. A simple example is given as follows.
Ex.1 Polynomial series
\[ f(z)=\sum_{n=0}^{\infty} z^n \]
which describes an analytic function for \(|z|<1\) but which diverges for \(|z|>1\). However, the function
\[ g(z)=\frac{1}{1-z} \]
is analytic over the whole plane (except at \(z=1\)), and it coincides with \(f(z)\) inside the unit circle.
Such a function \(g(z)\), which coincides with a given analytic \(f(z)\) over that region for which \(f(z)\) is defined by which also is analytic over some extension of that region, is said to be an analytic continuation of \(f(z)\). It is useful to think of \(f(z)\) and \(g(z)\) as being the same function and to consider that the formula defining \(f(z)\) failed to provide the values of \(f(z)\) in the extended region because of some defect in the mode of description rather than because of some limitation inherent in \(f(z)\) itself. [c.f. G.F.Carrier, M.Krook and C.E.Pearson, Functions of a Complex Variable, McGraw-Hill (1966), p.63]
Ex.2 Laplace transform
\[ \mathcal{L}[1]= \int_0^\infty \mathrm{d}t 1\cdot e^{i\omega t}=-\frac{1}{i\omega},\, \textrm{if } \Im(\omega)>0 \]
If you have a pure real frequency \(\omega\), then when you integrate \(v\) over the real axis, at \(v=\omega/k\) you will encounter a singular point. Actually, this integration is convergent if and only if \(\Im(\omega)>0\). \(-\frac{1}{i\omega}\) is the analytic continuation of \(f(\omega)\) for all complex \(\omega\) except \(\omega=0\).
To calculate the integral around singular points, we may take advantage of the Cauchy integral formula and the residual theorem.
Theorem 2.1 Cauchy integral
Let \(C_\epsilon\) be a circular arc of radius \(\epsilon\), centered at \(\alpha\), with subtended angle \(\theta_0\) in counterclockwise direction. Let \(f(z)\) be an analytic function on \(C_\epsilon+\)inside \(C_\epsilon\). Then
\[ \lim_{\epsilon\rightarrow0}\int_{c_\epsilon}\frac{f(z)dz}{z-\alpha}=i\theta_0 f(\alpha) \]
Proof: On \(C_\epsilon\), \(z=\alpha+\epsilon e^{i\theta}\), \(dz=i\epsilon e^{i\theta}\mathrm{d}\theta\).
\[ LHS=\lim_{\epsilon\rightarrow0}\int_{C_\epsilon}\frac{f(\alpha+\epsilon e^{i\theta})i\epsilon e^{i\theta}\mathrm{d}\theta}{\epsilon e^{i\theta}}=i\theta_0 f(\alpha). \] □
Theorem 2.2 Residue
Let \(f(z)\) be an analytic function on a closed contour \(C+\)inside \(C\). If point \(\alpha\) is inside \(C\), we have
\[ f(\alpha)=\frac{1}{2\pi i}\oint_c \frac{f(z)dz}{z-\alpha} \]
Proof:
\(\frac{f(z)}{z-\alpha}\) is analytic within region bounded by \(C+L_1-C_\epsilon+L_2\), where \(L_1\) and \(L_2\) are two paths that connects/breaks \(C\) and \(C_\epsilon\). Therefore
\[ \begin{aligned} \int_{C}+\int_{L_1}-\int_{C_\epsilon}+\int_{L_2}\frac{f(z)}{z-\alpha}dz=0 \\ \Rightarrow \oint_{C}\frac{f(z)}{z-\alpha}dz=\oint_{C_\epsilon}\frac{f(z)}{z-\alpha}dz=2\pi i f(\alpha) \textrm{ as }L_1\rightarrow -L_2,\epsilon\rightarrow0 . \end{aligned} \] □
There is also a purely algebraic proof available.
Note that the value of \(f(z)\) on \(C\) determines value of \(f(\alpha)\) for all \(\alpha\) within \(C\). This has a close relation to the potential theory. Actually, what Cauchy-Riemann condition says physically is that the potential flow is both irrotational and incompressible!
Theorem 2.3 Residual theorem
Let \(f(z)\) be an analytic function on \(C+\)inside \(C\). If point \(\alpha\) is inside \(C\), we have
\[ \oint_c \frac{f(z)dz}{z-\alpha}=2\pi i f(\alpha)\equiv 2\pi i \text{Res}\Big[ \frac{f(z)}{z-x};z=\alpha \Big] \tag{3.3}\] □
Khan Academy has a nice video on this. Applying this powerful theorem, we can calculate many integrals analytically which contain singular points.
Ex.3
\[ f(\omega)=\int_{-\infty}^{\infty}dv \frac{e^{iv}}{v-\omega}=2\pi ie^{i\omega},\,\Im(\omega)>0 \]
Pick a semi-circle contour \(C_R\) in the upper plane of complex v. Let \(C\) be a closed contour of a line along the real axis \(\Re(v)\) and the semi-circle \(C_R\). \(e^{iv}\) is analytic along and inside \(C\), so
\[ f(\omega)=\Big(\oint_C-\int_{C_R}\Big)\frac{dv e^{iv}}{v-\omega}=2\pi i e^{i\omega}-\int_{C_R}\frac{dv e^{iv}}{v-\omega}=2\pi i e^{i\omega} \textrm{ as } R\rightarrow \infty \]
\[ \Big( e^{iv}=e^{i(v_r+iv_i)}=e^{iv_r}e^{-v_i},v_i>0 ; v-\omega\rightarrow\infty\Big) \]
\(2\pi ie^{i\omega}\) is the analytic continuation of \(f(\omega)\) for all \(\omega\). Analytic continuation is achieved if we deform the contour integration in the complex \(v\) plane.
Ex.4
\[ \frac{\epsilon(\omega)}{\epsilon_0}=1-\frac{{\omega_{pe}}^2}{k^2}\chi(\omega) \]
where
\[ \begin{aligned} \chi(\omega)&=\int_{-\infty}^{\infty}dv \frac{\partial g/\partial v}{v-\omega/k},\ Im(\omega)>0 \\ &=\int_L dv\frac{\partial g(v)/\partial v}{v-\omega/k}, \textrm{for all complex $\omega$, as long as $L$ lies below $\omega$} \end{aligned} \]
Landau integral: pick a trajectory under the singular point in the complex plane to achieve the integration.
FIGURE NEEDED!
Let \(C_\epsilon\) be a small semi-circle under \(\omega/k\). Then
\[ \begin{aligned} \frac{\epsilon(\omega)}{\epsilon_0}&=1-\frac{{\omega_{pe}}^2}{k^2}\Big[ P\int_{-\infty}^{\infty}dv\frac{\partial g(v)\partial v}{v-\omega/k}+\int_{C_\epsilon}dv\frac{\partial g(v)\partial v}{v-\omega/k} \Big] \notag \\ &=1-\frac{{\omega_{pe}}^2}{k^2}\Big[ P\int_{-\infty}^{\infty}dv\frac{\partial g(v)\partial v}{v-\omega/k}+i\pi\frac{\partial g(v)}{\partial v}\big|_{v=\frac{\omega}{k}} \Big] \end{aligned} \]
where \(P\) denotes the principle value integral. This is the same as Equation 12.31 that will be discussed in Section 12.5.
3.5 Electromagnetic Four-Potential
An electromagnetic four-potential is a relativistic vector function from which the electromagnetic field can be derived. It combines both an electric scalar potential and a magnetic vector potential into a single four-vector.
As measured in a given frame of reference, and for a given gauge, the first component of the electromagnetic four-potential is conventionally taken to be the electric scalar potential, and the other three components make up the magnetic vector potential. While both the scalar and vector potential depend upon the frame, the electromagnetic four-potential is Lorentz covariant.
The electromagnetic four-potential can be defined as:
| SI units | Gaussian units |
|---|---|
| \(A^\alpha = \left( \frac{\phi}{c}, \mathbf{A} \right)\) | \(A^\alpha = \left( \phi, \mathbf{A} \right)\) |
in which \(\phi\) is the electric potential, and \(\mathbf{A}\) is the magnetic potential (a vector potential).
The electric and magnetic fields associated with these four-potentials are:
| SI units | Gaussian units |
|---|---|
| \(\mathbf{E} = -\nabla\phi - \frac{\partial\mathbf{A}}{\partial t}\) | \(\mathbf{E} = -\nabla\phi - \frac{1}{c}\frac{\partial\mathbf{A}}{\partial t}\) |
| \(\mathbf{B}=\nabla\times\mathbf{A}\) | \(\mathbf{B}=\nabla\times\mathbf{A}\) |
3.5.1 Multipolar gauge
A common problem is how to obtain the four-potential from EM field. This can be achieved in a simple way using the multipolar gauge (also known as the line gauge, point gauge or Poincaré gauge (named after Henri Poincaré)) \[ \mathbf{r}\cdot\mathbf{A} = 0 \tag{3.4}\] which says that the potential vector is perpendicular to the position vector \(\mathbf{r}\). With this we have \[ \begin{aligned} \mathbf{A}(\mathbf{r}, t) &= -\mathbf{r} \times \int_{0}^{1}\mathbf{B}(u\mathbf{r}, t) u\,\mathrm{d}u \\ \varphi(\mathbf{r}, t) &= -\mathbf{r} \cdot \int_{0}^{1}\mathbf{E}(u\mathbf{r}, t)\mathrm{d}u \end{aligned} \tag{3.5}\]
3.6 Helmholtz’s Theorem
Helmholtz’s theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field.
Let \(\mathbf{F}\) be a vector field on a bounded domain \(V \subseteq \mathbf{R}^3\), which is twice continuously differentiable, and let S be the surface that encloses the domain V. Then \(\mathbf{F}\) can be decomposed into a curl-free component and a divergence-free component:
\[ \mathbf{F}=\nabla \Phi +\nabla\times\mathbf{A} \]
where
\[ \begin{aligned} \Phi(\mathbf{r})&= \frac{1}{4\pi}\int_V\frac{\nabla^\prime\cdot\mathbf{F}^\prime(\mathbf{r}^\prime)}{|\mathbf{r}-\mathbf{r}^\prime|}dV^\prime -\frac{1}{4\pi}\oint_s \widehat{\mathbf{n}}^\prime\cdot\frac{\mathbf{F}(\mathbf{r}^\prime)}{|\mathbf{r}-\mathbf{r}^\prime|}dS^\prime \\ \mathbf{A} &= \frac{1}{4\pi}\int_V\frac{\nabla^\prime\times \mathbf{F}^\prime(\mathbf{r}^\prime)}{|\mathbf{r}-\mathbf{r}^\prime|}dV^\prime -\frac{1}{4\pi}\oint_s \widehat{\mathbf{n}}^\prime\times\frac{\mathbf{F}(\mathbf{r}^\prime)}{|\mathbf{r}-\mathbf{r}^\prime|}dS^\prime \end{aligned} \]
and \(\nabla^\prime\) is the nabla operator with respect to \(\mathbf{r}^\prime\), not \(\mathbf{r}\).
If \(V = \mathbf{R}^3\) and is therefore unbounded, and \(\mathbf{F}\) vanishes faster than \(1/r\) as \(r\rightarrow\infty\), then the second component of both scalar and vector potential are zero. That is,
\[ \begin{aligned} \Phi(\mathbf{r})&= \frac{1}{4\pi}\int_V\frac{\nabla^\prime\cdot\mathbf{F}^\prime(\mathbf{r}^\prime)}{|\mathbf{r}-\mathbf{r}^\prime|}dV^\prime \\ \mathbf{A} &= \frac{1}{4\pi}\int_V\frac{\nabla^\prime\times \mathbf{F}^\prime(\mathbf{r}^\prime)}{|\mathbf{r}-\mathbf{r}^\prime|}dV^\prime \end{aligned} \]
3.7 Toroidal and Poloidal Decomposition
The earliest use of these terms cited by the Oxford English Dictionary (OED) is by Walter M. Elsasser (1946) in the context of the generation of the Earth’s magnetic field by currents in the core, with “toroidal” being parallel to lines of latitude and “poloidal” being in the direction of the magnetic field (i.e. towards the poles).
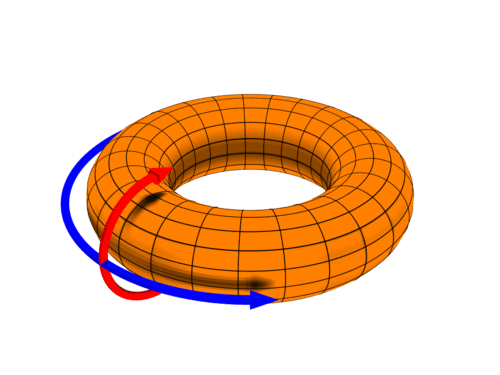
The OED also records the later usage of these terms in the context of toroidally confined plasmas, as encountered in magnetic confinement fusion. In the plasma context, the toroidal direction is the long way around the torus, the corresponding coordinate being denoted by z in the slab approximation or \(\zeta\) or \(\phi\) in magnetic coordinates; the poloidal direction is the short way around the torus, the corresponding coordinate being denoted by y in the slab approximation or \(\theta\) in magnetic coordinates. (The third direction, normal to the magnetic surfaces, is often called the “radial direction”, denoted by x in the slab approximation and variously \(\psi\), \(\chi\), r, \(\rho\), or \(s\) in magnetic coordinates.)
In vector calculus, a topic in pure and applied mathematics, a poloidal–toroidal decomposition is a restricted form of the Helmholtz decomposition. It is often used in the spherical coordinates analysis of solenoidal vector fields, for example, magnetic fields and incompressible fluids.
For a three-dimensional vector field \(\mathbf{F}\) with zero divergence
\[ \nabla\cdot\mathbf{F}=0 \]
This \(\mathbf{F}\) can be expressed as the sum of a toroidal field \(\mathbf{T}\) and poloidal vector field \(\mathbf{P}\)
\[ \mathbf{F} = \mathbf{T}+\mathbf{P} \]
where \(\widehat{r}\) is a radial vector in spherical coordinates \((r,\theta,\phi)\). The toroidal field is obtained from a scalar field, \(\psi(r,\theta,\phi)\) as the following curl,
\[ \mathbf{T}=\nabla\times(\widehat{r}\Psi(\mathbf{r})) \]
and the poloidal field is derived from another scalar field \(\phi(r,\theta,\phi)\) as a twice-iterated curl,
\[ \mathbf{P}=\nabla\times\nabla\times(\widehat{r}\Phi(\mathbf{r})) \]
This decomposition is symmetric in that the curl of a toroidal field is poloidal, and the curl of a poloidal field is toroidal. The poloidal–toroidal decomposition is unique if it is required that the average of the scalar fields \(\Psi\) and \(\Phi\) vanishes on every sphere of radius \(r\).
3.8 Magnetic Dipole Field
If there’s no current, \[ \nabla\times\mathbf{B}=\mu_0 \mathbf{J} = 0 \Rightarrow B=-\nabla V \]
The divergence free condition for magnetic field then yields a laplace equation \[ \Delta V = 0 \] for the Gauss potential \(V\). The general complex solution of Laplace equation in spherical coordinates is \[ \begin{aligned} V(\mathbf{r}) &= \sum_{l=0}^{\infty}\sum_{m=-l}^{l} \left( A_l r^l + B_l r^{-l-1} \right)P_l^m(\cos\theta)e^{-im\phi} \\ &= \sum_{l=0}^{\infty}\sum_{m=-l}^{l} \left( A_l r^l + B_l r^{-l-1} \right) Y_l^m(\theta, \phi) \end{aligned} \] where \[ Y_l^m(\theta,\phi) = P_l^m(\cos{\theta})e^{-im\phi} \] are the (complex) spherical harmonics. The indices l and m indicate degree and order of the function. The general real solution is \[ V(\mathbf{r}) = \sum_{l=0}^{\infty}\sum_{m=0}^{l} \left( A_l r^l + B_l r^{-l-1} \right)P_l^m(\cos\theta)\left[ S_m\sin{m\phi} + C_m\cos{m\phi} \right] \]
\(P_l^m\) are the associated Legendre polynomials. The first three terms of \(P_l^m(\cos\theta)\) are \[ \begin{aligned} P_0^0(\cos\theta) &= 1 \\ P_1^0(\cos\theta) &= \cos\theta \\ P_1^1(\cos\theta) &= -\sin\theta \end{aligned} \]
There are two parts in the real solution. The first part, starting with coefficients \(A_l\), represents the potential from an exterior source, which is analytic at \(r=0\) but diverges as \(r\rightarrow\infty\). The second part, starting with coefficients \(B_l\), represents the potential from an interior source, which is singular at \(r=0\) and finite as \(r\rightarrow\infty\).
Ex 1. Planet dipole field
For a planetary dipole field, we only consider the contribution from the internal source. The Gauss potential for the dipole reads \[ \begin{aligned} V &= \frac{1}{r^2}\big[ B_1C_0\cos\theta + B_1C_1\cos\phi\sin\theta + B_1S_1\sin\phi\sin\theta \big] \\ &= \frac{1}{r^2}\big[ G_{10}\cos\theta + G_{11}\cos\phi\sin\theta + H_{11}\sin\phi\sin\theta \big] \end{aligned} \]
If \(r\) is defined in the unit of planet radius, then the dipole moment \(\mathbf{m} = (G_{11},H_{11},G_{10})\) in Cartesian coordinates would have the SI unit of \([\text{T}\text{m}^3]\). We then have \[ \mathbf{B} = -\nabla V = -\nabla \Big[ \frac{\mathbf{m}\cdot\mathbf{r}}{r^3} \Big] = \frac{3(\mathbf{m}\cdot\widehat{r})\widehat{r}-\mathbf{m}}{r^3} \]
Often in literature we see dipole moments in the unit of \([\text{nT}]\,[\text{R}]^3\): this indicates that this dipole strength is equivalent to the equatorial field strength \(B_{\text{eq}}\) at the planet’s surface, and the field strength is scaled as \(r^{-3}\).
In SI units, we need to append additional coefficients \[ \mathbf{B} = \frac{\mu_0}{4\pi}\frac{3(\mathbf{m}\cdot\widehat{r})\widehat{r}-\mathbf{m}}{r^3} \] such that the dipole moment \(\mathbf{m}\) has the unit of \([\mathrm{A}]\,[\mathrm{m}]^2\), consistent with its physical meaning originated from a closed current loop.
In spherical coordinates \((r,\theta,\varphi)\) aligned with the dipole moment, \[ \mathbf{B} = \frac{\mu_0}{4\pi} \frac{m}{r^3} (-2\cos\theta, -\sin\theta, \,0) \tag{3.6}\]
It is usually convenient to work in terms of the latitude, \(\vartheta = \pi/2 - \theta\), rather than the polar angle, \(\theta\). An individual magnetic field-line satisfies the equation \[ r = r_\mathrm{eq}\,\cos^2\vartheta \] where \(r_\mathrm{eq}\) is the radial distance to the field line in the equatorial plane (\(\vartheta=0^\circ\)). It is conventional to label field lines using the L-shell parameter, \(L=r_\mathrm{eq}/R_E\). Here, \(R_E = 6.37\times 10^6\,\mathrm{m}\) is the Earth’s radius. Thus, the variation of the magnetic field-strength along a field line characterized by a given \(L\)-value is \[ B = \frac{B_E}{L^3} \frac{(1+3\,\sin^2\vartheta)^{1/2}}{\cos^6\vartheta} \] where \(B_E= \mu_0 M_E/(4\pi\, R_E^{~3}) = 3.11\times 10^{-5}\,\mathrm{T}\) is the equatorial magnetic field-strength on the Earth’s surface.
In Cartesian representation, \[ \mathbf{B} = \frac{\mu_0}{4\pi}\frac{1}{r^5} \begin{pmatrix} (3x^2-r^2) & 3xy & 3xz \\ 3yx & (3y^2-r^2) & 3yz \\ 3zx & 3zy & (3z^2-r^2) \end{pmatrix} \mathbf{m} \tag{3.7}\]
Note that \((x,y,z)\) and \(r\) are all normalized to the radius of the planet \(R\).
Ex 2. 2D dipole field
Let us consider the solution to the Laplace equation in polar coordinates \((r, \theta)\). Via separation of variable it can be shown that the general real solution takes the form \[ V = c_0\ln{r} + D_0 + \sum_{n=1}^\infty \left( A_n\cos{n\theta} + B_n\sin{n\theta} \right)\left( C_n r^n + D_n r^{-n} \right) \]
For a dipole field, we only consider \(n=1\) from the internal source. If we absorb \(D_1\) into \(A_1\) and \(B_1\), we have \[ V = (A_1\cos\theta + B_1\sin\theta)\frac{1}{r} = \frac{\mathbf{m}\cdot\mathbf{r}}{r^2} \] where the 2D magnetic moment is \(\mathbf{m}=(A_1, B_1)\).
Thus \[ \mathbf{B}_\mathrm{dipole,2D} = -\nabla V = \frac{2(\mathbf{m}\cdot\hat{r})\hat{r} - \mathbf{m}}{r^2} \tag{3.8}\] where the minus sign has been absorbed into the coefficients. 2D dipole scales as \(r^{-2}\).
Ex 3. Magnetic monopoles
Even though magnetic monopoles have not yet been observed in nature, there are some nice math tricks that allow us to approximate the magnetic dipole field as two opposite charged magnetic monopoles sitting close to each other. In 3D, the magnetic monopole would give a magnetic field \[ \mathbf{B}(\mathbf{r}) = \frac{\mu_0}{4\pi}\frac{g}{r^2}\hat{r} \] where \(g\) is the strength of the magnetic monopole in units of magnetic charge. In 2D, it would be \[ \mathbf{B}(\mathbf{r}) = C\frac{g}{r}\hat{r} \]
The analogy can be make from Coulomb’s law: an electric dipole field in 3D scales as \(r^{-3}\) when the electric monopole field scales as \(r^{-2}\).
3.9 Green’s Function
The Vlasov theory and the 2-fluid theory only tell us when instability will happen, but neither tell us the severity of instability. To know the magnitude of instability mathematically, we can introduce Green’s function \[ G(x,t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{ikx-i\omega(k) t}dk \] where \(t\) is the beam’s pulse length and \(x\) is the propagation distance. At \(t=0\), we have \[ \begin{aligned} G(x,0)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{ikx}dk=\frac{1}{2i\pi x}e^{ikx}\bigg|_{k=-\infty}^{k=\infty} \\ &=\lim_{k\rightarrow\infty}\frac{1}{2i\pi x}\big[ \cos{kx}+i\sin{kx}-\cos{kx}+i\sin{kx} \big] \\ &=\lim_{k\rightarrow\infty}\frac{1}{\pi}\frac{\sin{kx}}{x}=\delta(x) \end{aligned} \] where \(\delta(x)\) is the \(\delta\)-function.
The integral \(\int_0^{\infty}\frac{\sin x}{x}\mathrm{d}x\) is called the Dirichlet integral. It is a very famous and important generalized improper integral. Here at least you can see that \[ \int_{-\infty}^{\infty}G(x,0)=\frac{1}{\pi}\int_0^\infty \frac{\sin kx}{x}\mathrm{d}x=1\quad \textrm{and}\quad G(0,0)=\infty \]
3.10 Linearization
In linear wave analysis, we need to check how small perturbations evolve in the PDEs. For plasma physics, it is usually very useful to transform into a magnetic field guided coordinates, with the notation \(\parallel\) being parallel to the background magnetic field and \(\perp\) being perpendicular to the background magnetic field \(\mathbf{B}\). Besides the perturbation of plasma moments (i.e. density, velocity, pressure, etc.), we also need the perturbations to the magnitude of the magnetic field B and the unit vector \(\hat{\mathbf{b}}\). Linearzing \(B^2 = \mathbf{B}\cdot\mathbf{B}\), we find \[ \delta B = \hat{\mathbf{b}}\cdot\delta\mathbf{B} = \delta B_\parallel \tag{3.9}\]
Linearzing \(\hat{\mathbf{b}} = \mathbf{B}/B\), we obtain \[ \begin{aligned} \delta\hat{\mathbf{b}} = \delta\left(\frac{\mathbf{B}}{B}\right) = \frac{\delta\mathbf{B}B - \delta B\mathbf{B}}{B^2} = \frac{\delta\mathbf{B}}{B} - \frac{\delta \mathbf{B}_\parallel}{B} = \frac{\delta \mathbf{B}_\perp}{B} \end{aligned} \tag{3.10}\]
The divergence-free of magnetic field gives \[ \mathbf{k}\cdot\delta\mathbf{B} = k_\parallel \delta B_\parallel + k_\perp \delta B_\perp = 0 \]
Thus \[ \mathbf{k}\cdot\hat{\mathbf{b}} = \mathbf{k}\cdot\frac{\delta \mathbf{B}_\perp}{B} = \frac{k_\perp \delta B_\perp}{B} = -k_\parallel\frac{\delta B_\parallel}{B} = -k_\parallel\frac{\delta B}{B} \tag{3.11}\]
These seemingly trivial relations have profound implications in physics. Equation 3.9 tells us that the perturbation of magnetic field magnitude has only contribution from the parallel component, which is why in satellite observations people only look at parallel perturbations for compressional wave modes. Equation 3.10 tells us that the perturbation in the unit vector is only related to the perpendicular fluctuations.
3.11 Wave Equations
The waves in plasma physics is governed by second order ODEs. Here we list some second order ODEs that has been studied mostly in plasma physics.
- Schrödinger Equation:
\[ \frac{\mathrm{d}^2\varphi}{\mathrm{d}x^2} + \frac{2m}{\hbar^2}\big[ E-U(x)\big]\varphi= 0 \]
Schrödinger Equation appears in the nonlinear wave studies (Chapter 17).
- Shear Alfvén wave:
\[ \frac{\mathrm{d}}{\mathrm{d}x}\Big\{ \rho_0 \big[ \omega^2 - (\mathbf{k}\cdot\mathbf{v}_A(x))^2 \big]\frac{dE}{\mathrm{d}x} \Big\} - k^2\rho_0 \big[ \omega^2 - (\mathbf{k}\cdot\mathbf{v}_A)^2 - g\frac{1}{\rho_0}\frac{\mathrm{d}\rho_0}{\mathrm{d}x} \big]E = 0 \]
The Shear Alfvén wave equation appears in nonuniform ideal MHD (Equation 10.30, Equation 16.8).
- EM waves in non-magnetized plasma, O mode:
\[ \frac{\mathrm{d}^2 E}{\mathrm{d}x^2} + \frac{\omega^2}{c^2} \Big[ 1-\frac{{\omega_{pe}(x)}^2}{\omega^2} \Big]E = 0 \tag{3.12}\]
- Electron cyclotron resonance heating (ECRH):
\[ \frac{\mathrm{d}^2 E}{\mathrm{d}x^2} + \frac{\omega^2}{c^2} \Big[ 1-\frac{{\omega_{pe}(x)}^2}{\omega(\omega-\Omega_e(x))} \Big]E = 0 \]
In general, a second order ODE \[ \frac{\mathrm{d}^2 u(x)}{\mathrm{d}x^2} + a_1(x)\frac{du(x)}{\mathrm{d}x} + a_2(x)u(x) = 0 \] can be rewritten to get rid of the first derivative. Let \[ u(x) = E(x) e^{-\frac{1}{2}\int^x a_1(x)\mathrm{d}x} \] we have \[ \frac{\mathrm{d}^2 E(x)}{\mathrm{d}x^2} + k^2(x) E(x) = 0 \tag{3.13}\] where \[ k^2(x) = a_2(x) - \frac{{a_1}^2}{4} -\frac{1}{2}\frac{\mathrm{d} a_1(x)}{\mathrm{d}x} \]
Note that the lower bound of the integral is left on purpose to account for a constant. We will concentrate at special points, i.e. zeros (cutoff) and poles (resonance) of \(k^2(x)\equiv \frac{\omega^2}{c^2}n^2(x)\).
First, we will introduce Wentzel–Kramers–Brillouin-Jeffreys (WKBJ) solution to Equation 3.13: \[ E(x) \sim \frac{1}{\sqrt{k(x)}}e^{\pm i\int^x k(x^\prime)\mathrm{d}x^\prime}. \]
Proof.
For simplicity, here we use a simple harmonic oscillation analogy. Consider \[ \frac{\mathrm{d}^2 x(t)}{\mathrm{d}t^2} + \Omega^2(t)x(t) = 0 \]
Assume \(\Omega \gg 1\), and \(T\) is the time scale over which \(\Omega\) changes appreciably. We would anticipate solutions like \[ \begin{aligned} &x(t)\sim e^{\pm i \Phi(t)} \\ &\dot{x}(t) \sim \pm i \dot{\Phi}(t) x(t) \\ &\ddot{x}(t) \sim - \dot{\Phi}^2(t) x(t) \cancel{\pm i \ddot{\Phi}(t)x(t)} \\ \Rightarrow &\dot{\Phi}(t) = \Omega(t),\ \text{or } \Phi(t) = \int^t \Omega(t^\prime) \mathrm{d}t^\prime + \text{const.} \end{aligned} \]
Write \(x(t) = A(t)\sin{[\Phi(t)]}\), where \(A(t)\) is slowly varying in time, \(\dot{A}(t)\ll \Omega A\), which is almost a periodic motion. From adiabatic theory in classical mechanics, \(\oint pdq \simeq \text{const.}\), we have \[ \begin{aligned} \oint mv_x \mathrm{d} x \simeq \text{const.} \\ \oint m\dot{x}\dot{x}\mathrm{d}t \simeq \text{const.} \end{aligned} \]
Then in a period \(2\pi/\Omega\), \[ \frac{2\pi}{\Omega}\oint m\dot{x}^2dt =\frac{2\pi}{\Omega}\oint mA^2 \Omega^2\cos^2\Phi \mathrm{d}t \simeq \text{const.} \] which leads to \[ mA^2\Omega \simeq \text{const.},\ A\sim\frac{1}{\sqrt{\Omega}} \]
Thus the general form of solution can be written as \[ x(t)\sim\frac{1}{\sqrt{\Omega}}e^{\pm i \Phi(t)} \sim\frac{1}{\sqrt{\Omega}} e^{\pm i \int^t \Omega(t^\prime)\mathrm{d}t^\prime+\text{const.}} \]
□
Note:
- There is no lower limit to the integral, because it is like adding a constant.
- This solution is valid if \(k\cdot L > O(3)\), where \(L\) is the length scale over which \(k^2(x)\) changes appreciably. (???)Formally the condition should be \(kL\gg 1\). Apparently near resonance (\(k\rightarrow\infty\)), the condition breaks down, then how do we reconcile the solution? There are more discussions coming up and applications in Chapter 10 and Chapter 16.
3.11.1 Airy Function
We want to develop a general method for cut-off and resonance. Away from the turning point \(x_t\), \[ E_{\text{WKBJ}}(x) \sim \frac{1}{\sqrt{k(x)}}e^{\pm i\int^x k(x)\mathrm{d}x} \]
Near \(x=x_t\), we can use a linear approximation for \(k^2(x)\) (first term in the Taylor expansion), \[ k^2(x) \approx -{k_0}^2 a(x-x_t) \]
Then \[ \begin{aligned} \frac{\mathrm{d}^2 E}{\mathrm{d}x^2} + k^2(x)E &= 0 \\ \frac{\mathrm{d}^2 E}{\mathrm{d}x^2} - {k_0}^2 a (x-x_t) E &= 0 \end{aligned} \]
Let \(\frac{x-x_t}{l}=\zeta\), we have \[ \frac{\mathrm{d}^2 E}{\mathrm{d}\zeta^2} - l^2 {k_0}^2 a l \zeta E(\zeta) = 0 \]
If we choose \(l\) s.t. \(l^3 {k_0}^2 a =1\) (non-dimensional treatment), we obtain \[ \frac{\mathrm{d}^2 E}{\mathrm{d}\zeta^2} - \zeta E(\zeta) = 0 \tag{3.14}\]
which is equivalent to the case where \(k^2(\zeta)=-\zeta\) that shows the linear approximation. Equation 3.14, known as the Airy equation or Stokes equation, is the simplest second-order linear differential equation with a turning point (a point where the character of the solutions changes from oscillatory to exponential). From the WKBJ theory, we get the solution \[ E_{\text{WKBJ}} \sim \frac{1}{\sqrt{k(x)}}e^{\pm i\int^x k(x^\prime)\mathrm{d}x^\prime} = \left\{ \begin{array}{rl} \zeta^{-1/4}e^{\mp\frac{2}{3}\zeta^{3/2}} & \text{if } \zeta > 0 \\ (-\zeta)^{-1/4}e^{\pm i \frac{2}{3}(-\zeta)^{3/2}} & \text{if } \zeta < 0 \end{array} \right. \]
Note that the solution blows up at \(\zeta=0\) (turning point) miserably. For \(\zeta>0\), one solution is exponentially decay while the other is exponentially growing; for \(\zeta<0\), the two solutions are oscillatory. Solutions can also be found as series in ascending powers of \(\zeta\) by the standard method. Assume that a solution is \(E=a_0+a_1\zeta+a_2\zeta^2+...\) Substitute this in Stokes Equation and equate powers of \(\zeta\) will give relations between the constants \(a_0,a_1,a_2\),etc., and lead finally to \[ \begin{aligned} E = &a_0\Big\{ 1+\frac{\zeta^3}{3\cdot2} +\frac{\zeta^6}{6\cdot5\cdot3\cdot2} + \frac{\zeta^9}{9\cdot8\cdot6\cdot5\cdot3\cdot2} + ... \Big\} \\ &+a_1\Big\{ \zeta+\frac{\zeta^4}{4\cdot3} +\frac{\zeta^7}{7\cdot6\cdot4\cdot3} + \frac{\zeta^{10}}{10\cdot9\cdot7\cdot6\cdot4\cdot3} + ... \Big\} \end{aligned} \] which contains the two arbitrary constants \(a_0\) and \(a_1\), and is therefore the most general solution. The series are convergent for all \(\zeta\), which confirms that every solution of Stokes Equation is finite, continuous and single valued.
This form is usually not easy to interpret in physical sense. Besides this, we can find a more useful solution to Equation 3.14 using the integral representation. An equivalent but maybe more intuitive approach is to solve Equation 3.14 with Fourier transform; a coefficient \(2\pi\) naturally appears. Both approaches reach the same results.
Write \[ E(\zeta) = \int_a^b \mathrm{d}t e^{t\zeta} f(t) \] where the integral represents a path in the complex t plane from \(a\) to \(b\). Then \[ \begin{aligned} \frac{\mathrm{d}^2 E}{\mathrm{d}\zeta^2} &= \int_a^b \mathrm{d}t\ t^2 e^{t\zeta} f(t) \\ \zeta E(\zeta) &= \int_a^b \mathrm{d}t \zeta e^{t\zeta} f(t) = \int_a^b \mathrm{d}t \frac{\mathrm{d}}{\mathrm{d}t}(e^{t\zeta}) f(t) \\ &=e^{t\zeta} f(t) \Big|_a^b -\int_a^b dte^{t\zeta} f^\prime(t) \end{aligned} \]
The limits \(a,b\) are be chosen so that the first term vanishes at both limits. Then Equation 3.14 is satisfied if
\[ \left\{ \begin{array}{l} e^{t\zeta} f(t) \Big|_a^b = 0\\ t^2 f(t) = -\frac{\mathrm{d} f(t)}{\mathrm{d}t} \Rightarrow f(t) = Ae^{-\frac{1}{3}t^3} \end{array} \right. \]
where \(A\) is a constant. The solution is now written as
\[ E(\zeta) = \int_a^b \mathrm{d}t Ae^{t\zeta-\frac{1}{3}t^3} \]
The limits \(a\) and \(b\) must therefore be chosen so that \(e^{t\zeta-\frac{1}{3}t^3}\) is zero for both. (Note that \(\zeta\) is a constant.) This is only possible if \(t=\infty\) and the real part of \(t^3\) is positive:
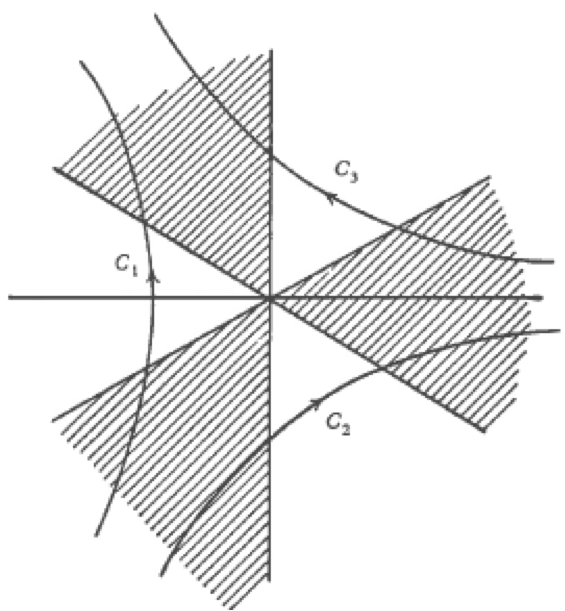
\[ \begin{aligned} \Re(t^3) > 0 \Leftrightarrow 2\pi n -\frac{1}{2}\pi < \arg{t^3} < 2\pi n + \frac{1}{2}\pi \\ \Leftrightarrow 2\pi n -\frac{1}{2}\pi < 3 \arg{t} < 2\pi n + \frac{1}{2}\pi \end{aligned} \]
where \(n\) is an integer. Figure 3.2 is a diagram of the complex t-plane, and \(a\) and \(b\) must each be at \(\infty\) in one of the shaded sectors. They cannot both be in the same sector, for then the integral would be zero. Hence the contour may be chosen in three ways, as shown by the three curves \(C_1,C_2,C_3\), and the solution would be
\[ E(\zeta) = \int_{C_1,C_2,C_3} \mathrm{d}t\ e^{t\zeta-\frac{1}{3}t^3} \]
This might appear at first to give three independent solutions, but the contour \(C_1\) and be distorted so as to coincide with the two contours \(C_2+C_3\), so that
\[ \int_{C_1} = \int_{C_2} + \int_{C_3} \]
and therefore there are only two independent solutions.
Proof.
Note that:
- \(e^{A}\neq 0\ \forall |A|<\infty\);
- \(e^{A}=0 \Leftrightarrow\, A\rightarrow \infty\,\text{and}\,\Re(A)<0\).
Therefore we have
\[ e^{-\frac{1}{3}t^3}\rightarrow 0\,\text{as}\, t\rightarrow \infty\,\text{and}\,\Re\Big(\frac{1}{3}t^3\Big)>0 \] In polar coordinates, let \(t=|t|e^{i\theta}\). Then
\[ t^3 = |t|^3 e^{i3\theta} = |t|^3 \big( \cos{3\theta} + i\sin{3\theta} \big) \]
\[ \Re\Big(\frac{1}{3}t^3\Big)>0 \iff \cos{3\theta}>0 \iff 3\theta \in (-\frac{\pi}{2},\frac{\pi}{2}),\ (\frac{3\pi}{2},\frac{5\pi}{2}),\ (-\frac{3\pi}{2},-\frac{5}{2}\pi) \]
□
Jeffreys (1956) defines two special Airy functions \(Ai(x), Bi(x)\) as follows
\[ \begin{aligned} Ai(\zeta) &= \frac{1}{2\pi i}\int_{C_1} \mathrm{d}t e^{-\frac{1}{3}t^3 + \zeta t} \\ Bi(\zeta) &= \frac{1}{2\pi} \Big[\int_{C_2}+\int_{C_3}\Big]\mathrm{d}t e^{-\frac{1}{3}t^3 + \zeta t} \end{aligned} \tag{3.15}\]
Obviously he took the Fourier transform such that a coefficient \(2\pi\) naturally appears. In Equation 3.15, the contour \(C_1\) can be distorted so as to coincide with the imaginary t-axis for almost its whole length. It must be displaced slightly to the left of this axis at its ends to remain in the shaded region at infinity. Let \(t=is\). Then the Airy function of the first kind in Equation 3.15 becomes
\[ \begin{aligned} Ai(\zeta) &= \frac{1}{2\pi}\int_{-\infty}^{\infty}e^{i(\zeta s+\frac{1}{3}s^3)}ds \\ &=\frac{1}{\pi}\int_{0}^{\infty}\cos\Big(\zeta s+\frac{1}{3}s^3\Big)ds \end{aligned} \]
It is known as the Airy integral, which is the solution for \(y\rightarrow 0\) as \(x\rightarrow\infty\). The other linearly independent solution, the Airy function of the second kind, denoted \(Bi(x)\), is defined as the solution with the same amplitude of oscillation as \(Ai(x)\) as \(x\rightarrow -\infty\) which differs in phase by \(\pi/2\):
\[ Bi(\zeta) = \frac{1}{\pi}\int_{0}^{\infty}\Big[e^{-\frac{s^3}{3}+s\zeta} + \sin\Big(\zeta s+\frac{1}{3}s^3\Big)\Big]ds \]
\(Ai(x)\) and \(Bi(x)\) are shown in ?fig-airy.
KeyNotes.plot_airy()As an interesting experiment, we can check if \(Ai(x)\) is recovered from solving the second order ODE numerically:
@sco KeyNotes.plot_airy_ode()Here we start from the right boundary and move towards the left.
Now, to find approximations for Airy functions, we use the method of steepest descent. This approximation is based on the assumption that major contribution to the integral is from near the saddle point. As an example of saddle point, consider a complex function \(\exp{f(z)}=e^{-z^2}\), where \(z=x+i y\).
- If \(z=\text{real} = x\), \(e^{-z^2}=e^{-x^2}\);
- If \(z=\text{imag}=iy\), \(e^{-z^2}=e^{y^2}\).
The procedure goes as follows:
- Detour path of integral s.t. it passes through the saddle point of the integral, along the direction of steepest descent.
- Obtain major contribution by integrating the Gaussian function.
\[ I=\int_C \mathrm{d}t e^{f(t)},\quad f(t) = f(t_s) + (t-t_s)f^\prime(t_s) + \frac{1}{2}(t-t_s)^2 f^{\prime\prime}(t_s) + ... \] where \(f^\prime(t_s)=0\) at the saddle point \(t=t_s\) simplifies \(I\) to the integral of a Gaussian function.
For \(Ai(\zeta)\), \[ \begin{aligned} f(t) &= t\zeta -\frac{1}{3}t^3 \\ f^\prime(t_s)& = \zeta - {t_s}^2 = 0 \\ f^{\prime\prime}(t_s)& = -2t_s \end{aligned} \]
Consider \(\zeta>0\) (where the solution is either exponentially decaying or growing.) Then \[ \begin{aligned} t_{s1} = -\sqrt{\zeta},\quad t_{s2} = \sqrt{\zeta} \\ f(t_{s1}) = -\frac{2}{3}\zeta^{3/2},\quad f^{\prime\prime}(t_{s1}) = 2\zeta^{1/2} \end{aligned} \] So \[ \begin{aligned} Ai(\zeta) &= \frac{1}{2\pi i} \int_{C_1} \mathrm{d}t\ e^{-\frac{2}{3}\zeta^{3/2}+\zeta^{1/2}(t-t_s)^2}+... \\ &\approx\frac{1}{2\pi i} e^{-\frac{2}{3}\zeta^{3/2}}\int_{C_1}\mathrm{d}t\ e^{\sqrt{\zeta}(t-t_s)^2} \end{aligned} \]
Let \(e^{\sqrt{\zeta}(t-t_s)^2}=e^{-\rho^2}\), where \(\rho=\text{real}\) is the direction of steepest descent, and \(\rho=\text{imag}\) is the direction of steepest ascent.
\[ \begin{aligned} i\rho &= \pm \zeta^{1/4} (t-t_s) \\ \mathrm{d}t&=\frac{i \mathrm{d}\rho}{\zeta^{1/4}} \Rightarrow\ \mathrm{d}t \text{ is purely imaginary along steepest descent.} \end{aligned} \]
Then for \(\zeta>0\) \[ \begin{aligned} Ai(\zeta) &= \frac{1}{2\pi i}e^{-\frac{2}{3}\zeta^{3/2}}\int_{-\infty}^{\infty}\frac{id\rho}{\zeta^{1/4}}e^{-\rho^2} \nonumber \\ &=\frac{1}{2\sqrt{\pi}\zeta^{1/4}}e^{-\frac{2}{3}\zeta^{3/2}} \text{ as}\ \zeta\rightarrow \infty \end{aligned} \tag{3.16}\]
The ratio of accuracy is shown in the following table (LABEL???). In practice, it is already a very good approximation when \(\zeta>3\). (think of \(kL\gg 3\) for WKBJ solution! ???)
| \(\zeta\) | 1 | 2 | 3 | 6 | \(\infty\) |
|---|---|---|---|---|---|
| ratio | 0.934 | 0.972 | 0.983 | 0.993 | 1 |
Now, consider \(\zeta<0\). When \(\zeta\rightarrow-\infty\), we anticipate oscillating behavior of \(Ai(\zeta)\). \(\zeta=-|\zeta|\), \[ \begin{aligned} &\left\{ \begin{array}{rl} f(t) &= \zeta t-\frac{1}{3}t^3 = -t|\zeta| - \frac{1}{3}t^3 \\ f^\prime(t) &= -|\zeta| - t^2 = 0 \\ f^{\prime\prime}(t) &= -2t \end{array} \right. \\ \Rightarrow &f(t_{s1}) = i\frac{2}{3}|\zeta|^{3/2} \\ &f^{\prime\prime}(t_{s1}) = 2i\sqrt{|\zeta|} \end{aligned} \] so the contribution from \(t_{s1}\) is \[ \frac{1}{2\pi i}e^{i\frac{2}{3}|\zeta|^{3/2}}\int_{t_{s1}} e^{\frac{1}{2}(2i\sqrt{|\zeta|})(t-t_s)^2+...} \]
Let \(-\rho^2=i\sqrt{|\zeta|}(t-t_{s1})^2\), differentiate on both sides to get \[ \mathrm{d}t = \pm\frac{e^{i\pi/4}}{|\zeta|^{1/4}}\mathrm{d}\rho \]
Again, \(\rho=\text{real}\) is the direction of steepest descent at \(t=t_{s1}\). Do the same to \(t_{s2}\), then by summing them up we have for \(\zeta<0\), \[ \begin{aligned} Ai(\zeta) &\approx \frac{1}{2\pi i} \Big[ e^{i\frac{2}{3}|\zeta|^{3/2}}\int_{-\infty}^{\infty}\frac{e^{i\pi/4}}{|\zeta|^{1/4}}\mathrm{d}\rho e^{-\rho^2} - e^{-i\frac{2}{3}|\zeta|^{3/2}}\int_{-\infty}^{\infty}\frac{e^{-i\pi/4}}{|\zeta|^{1/4}}\mathrm{d}\rho e^{-\rho^2} \Big] \\ &= \frac{1}{2\pi i} \Big[ \frac{e^{i\frac{2}{3}|\zeta|^{3/2}+i\pi/4}}{{|\zeta|^{1/4}}} \sqrt{\pi} - \frac{e^{-i\frac{2}{3}|\zeta|^{3/2}-i\pi/4}}{{|\zeta|^{1/4}}} \sqrt{\pi} \Big] \end{aligned} \tag{3.17}\]
An interesting application of the gradient descent method is to find Stirling’s approximation. Mathematically, we can proof that \[ n! =\int_0^\infty \mathrm{d}t\ e^{-t}t^n = \int_0^\infty \mathrm{d}t\ e^{-t+n\ln{t}} \equiv \int_0^\infty \mathrm{d}t\ e^{f(t)} \] and by following the steepest descent method, \[ \begin{aligned} f(t) &= -t +n\ln{t} \\ f^\prime(t) &= -1 + n\frac{1}{t}=0 \\ f^{\prime\prime}(t) &= -n\frac{1}{t^2} \end{aligned} \]
we can find the approximation Stirling formula \[ \begin{aligned} n! &\approx \int_0^\infty \mathrm{d}t\ e^{-n+n\ln{n}-\frac{1}{2n}(t-t_s)^2} \\ &=e^{-n}n^n \int_0^\infty \mathrm{d}t\ e^{-\frac{1}{2n}(t-t_s)^2} \\ &=\sqrt{2n\pi}e^{-n}n^n \end{aligned} \]
The following table (LABEL???) show the goodness of approximation of Stirling formula. In practice, it is already a very good approximation when \(n>3\).
| \(\zeta\) | 1 | 2 | 3 | 10 | \(\infty\) |
|---|---|---|---|---|---|
| ratio | 0.922 | 0.9595 | 0.973 | 0.9917 | 1 |
See (Budden 1961) Chapter 15: The Airy Integral Function, And The Stokes Phenomenon for more details.
3.11.2 Uniformly Valid WKBJ Solution Across the Turning Point
In this section, we present the WKBJ solution that is uniformly valid everywhere, even at the turning point.
Consider the standard equation,
\[ \frac{\mathrm{d}^2E(x)}{\mathrm{d}x^2}+k^2(x)E(x) = 0 \]
Let \(x=0\) be the turning point, i.e. we assume that \(k^2(x)\) is a monotonically decreasing function of \(x\) with \(k(0)=0\). For the region \(x>0\), we first identify the exponentially decaying factor of the Airy function, \(Ai(\zeta)\), to be the phase integral in the WKBJ solution:
\[ -\frac{2}{3}\zeta^{3/2} = i \int_0^x k(x^\prime)\mathrm{d}x^\prime \]
Note that this yields \(\zeta=\zeta(x)\), a known function of x (I confuse myself later about \(\zeta\) and \(x\)…). The branch for \(\zeta(x)\) is to be chosen so that for \(x>0\), \(\zeta\) is real and positive.
We next verify that the uniformly valid solution to the standard equation is simply
\[ E(x) = \frac{1}{\sqrt{\zeta^\prime(x)}}Ai(\zeta) \tag{3.18}\]
where the prime denotes a derivative. For large values of \(\zeta\), we can use the asymptotic formula of \(Ai\) Equation 3.16, and notice that
\[ \begin{aligned} -\zeta^{1/2}\zeta^\prime = ik(x) \\ \zeta^\prime(x) = -i \frac{k(x)}{\zeta^{1/2}} \end{aligned} \]
we can see that Equation 3.18 reduces to the standard WKBJ solutions for large values of \(\zeta\)
\[ E(x)= \frac{1}{\sqrt{\zeta^\prime(x)}}Ai(\zeta) \sim \frac{1}{\sqrt{k(x)}} e^{-\frac{2}{3}\zeta^{3/2}} = \frac{1}{\sqrt{k(x)}}e^{ i \int_0^x k(x^\prime)\mathrm{d}x^\prime} \]
We can also show that Equation 3.18 is valid for small values of \(\zeta\), i.e. near the turning point at \(x=0\). (Hint: Near \(x=0\), \(k^2(x)\) may be approximated by a linear function of \(x\). This linear approximation then yields \(\zeta(x)\) as a linear function of \(x\) according to Equation 3.18.)
Ex. Choose a smooth plasma density profile which monotonically increases with \(x\) s.t.
\[ \frac{\omega_{pe}^2(x)}{\omega^2} = 1 + \tanh{x} \]
and launch a wave of frequency \(\omega\) from \(x=-\infty\), the vacuum region, toward the positive \(x\)-direction with \(\frac{\omega^2}{c^2} = 10 \text{m}^{-2}\). (This is like launching a wave from low \(B\) region into high \(B\) region.) Numerically integrate the wave equation Equation 3.12,
\[ \frac{\mathrm{d}^2 E}{\mathrm{d}x^2} + \frac{\omega^2}{c^2} \Big[ 1-\frac{{\omega_{pe}(x)}^2}{\omega^2} \Big]E = 0 \]
from some large positive values of \(x\), we get the results in Figure 3.3.
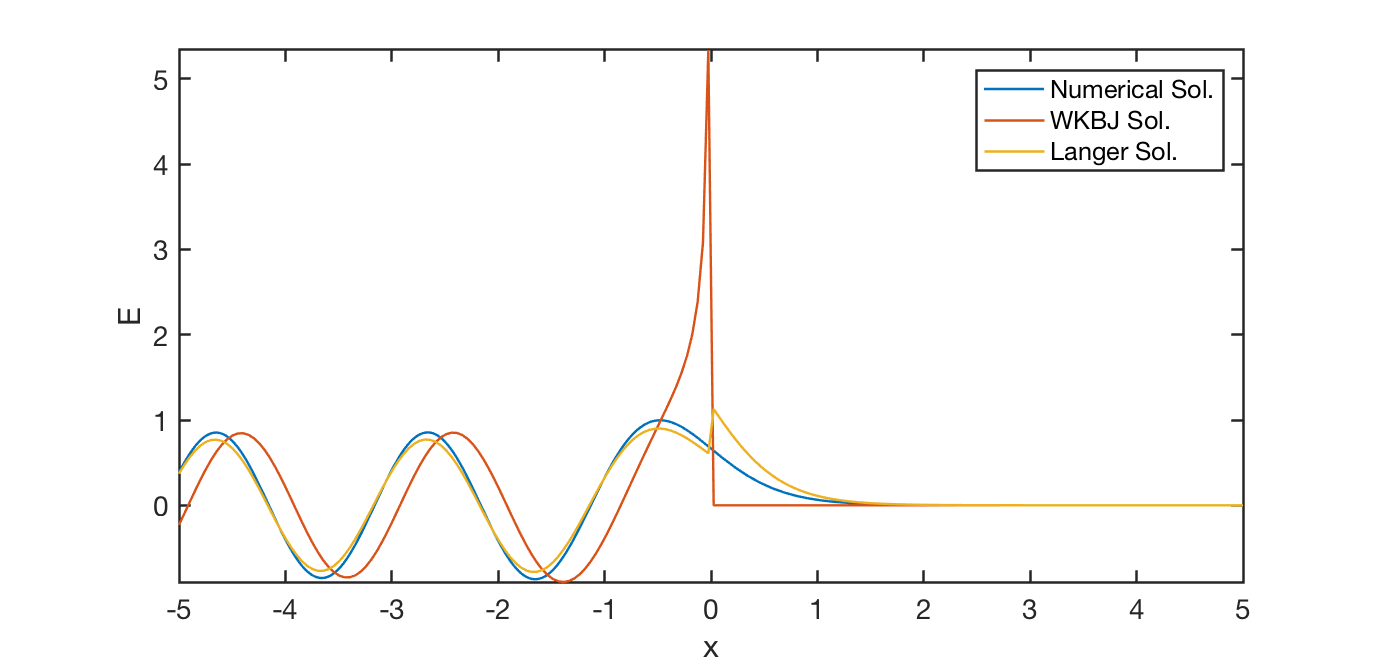
We know that away from \(x_t\), WKBJ solution works. To the left of \(x_t\) (with \(\zeta<-3\)), Equation 3.17 gives
\[ Ai(\zeta) = \frac{1}{2i\sqrt{\pi}|\zeta|^{1/4}}\Big[ e^{i \frac{2}{3}|\zeta|^{3/2}+i\frac{\pi}{4}} - e^{-\frac{2}{3}|\zeta|^{3/2}-i\frac{\pi}{4}} \Big] \]
Choose the branch s.t. \(\zeta{x}>0\) if \(x>x_t\); \(\zeta(x)<0\) if \(x<x_t\).
\[ \begin{aligned} E(x) &= \frac{1}{\sqrt{\zeta^\prime(x)}}Ai(\zeta) \\ &= \frac{C_3}{\sqrt{k(x)/|\zeta|^{1/2}}}\frac{1}{|\zeta|^{1/4}}\Big\{ e^{i \frac{2}{3}|\zeta|^{3/2}+i\frac{\pi}{4}} - c.c \Big\} \\ &= \frac{C_3}{\sqrt{k(x)}}\Big\{ e^{i(-\int_{x_t}^x k(x^\prime)\mathrm{d}x^\prime)+i\frac{\pi}{4}} - c.c \Big\} \\ &=\frac{C_3}{\sqrt{k(x)}}\Big\{ e^{-i\int_{x_t}^a k(x^\prime)\mathrm{d}x^\prime - i\int_a^x k(x^\prime)\mathrm{d}x^\prime+i\frac{\pi}{4}} -c.c \Big\} \\ &=\frac{C_4}{\sqrt{k(x)}}\Big\{ e^{-i \int_a^x k(x^\prime)\mathrm{d}x^\prime}-e^{i\int_{x_t}^a k(x^\prime)\mathrm{d}x^\prime } e^{2i\int_{x_t}^a k(x^\prime)\mathrm{d}x^\prime -i\frac{\pi}{2}} \Big\} \\ &=\frac{C_4}{\sqrt{k(x)}}\Big\{ e^{-i\int_a^x k \mathrm{d}x^\prime} + R\cdot e^{i\int_a^x k \mathrm{d}x^\prime} \Big\}, \end{aligned} \]
where
\[ C_4 = C_3 \cdot e^{-i \int_{x_t}^a k \mathrm{d}x^\prime + i\frac{\pi}{4}} \]
and
\[ R = -e^{2i\int_{x_t}^a k \mathrm{d}x^\prime - i\frac{\pi}{2}} = i e^{2i\int_{x_t}^a k \mathrm{d}x^\prime} = i e^{-2i \int_{a}^{x_t}kdx^\prime} \]
is the reflection coefficient at \(x=a\).
3.11.3 Stokes Phenomenon
In complex analysis the Stokes phenomenon is that the asymptotic behavior of functions can differ in different regions of the complex plane, and that these differences can be described in a quantitative way.
Ex. For the simple wave equation
\[ \frac{\mathrm{d}^2 E}{dz^2} - E = 0 \]
the solution can be given in various forms
\[ \begin{aligned} E=e^z,e^{-z},\cosh{z},\sinh{z} \\ E = \cosh{z}=\frac{1}{2}(e^z+e^{-z}) \Rightarrow \left\{ \begin{array}{rl} &E\sim\frac{1}{2}e^z\, z\rightarrow\infty \\ &E\sim\frac{1}{2}e^{-z}\, z\rightarrow-\infty \end{array} \right. \\ E = \sinh{z}=\frac{1}{2}(e^z-e^{-z}) \Rightarrow \left\{ \begin{array}{rl} &E\sim\frac{1}{2}e^z\, z\rightarrow\infty \\ &E\sim\frac{-1}{2}e^{-z}\, z\rightarrow-\infty \end{array} \right. \end{aligned} \]
Note that if a solution is exponentially growing in one direction, its asymptotic solution can contain an arbitrary amount of the exponentially decaying solution; that is, specifying an asymptotic growing solution in one direction cannot completely specify the solution in the entire complex plane.
The two linearly independent approximate solutions to Airy Equation 3.14 are the Airy function approximations from WKBJ method:
\[ \begin{aligned} &\frac{\mathrm{d}^2 E}{\mathrm{d}\zeta^2} - \zeta E = 0 \\ \Rightarrow &E(\zeta) = \left\{ \begin{array}{rl} &Ai(\zeta)\sim \frac{1}{2\sqrt{\pi}\zeta^{1/4}}e^{-\frac{2}{3}\zeta^{3/2}},\quad \zeta>0 \\ &Bi(\zeta)\sim \frac{1}{2\sqrt{\pi}\zeta^{1/4}}e^{\frac{2}{3}\zeta^{3/2}},\quad \zeta>0 \end{array} \right. \\ \end{aligned} \]
which is very accurate for \(\zeta>3\) (see previous section).
Stokes found that you can add an arbitrary amount of \(Ai(\zeta)\) to \(Bi(\zeta)\) without changing the behaviour of solution. (\(Ai(\zeta)<O(\zeta^{-1})\)???)
We want to find \(\zeta\) s.t. \(E_{\text{WKBJ}}\) is purely growing/decaying exponentially:
\[ \begin{aligned} \zeta^{3/2} \text{is purely real} \iff (|\zeta|e^{i\theta})^{3/2} \text{is purely real} \iff \sin{\frac{3}{2}\theta} = 0,\ \theta=0,\pm\frac{2}{3}\pi,\pm\frac{4}{3}\pi \end{aligned} \]
The lines in the complex plane on which WKBJ solution is purely growing/decaying exponentially are called Stokes lines (Figure 3.4). It is accompanied with anti-Stokes lines (in the opposite direction to Stokes lines), on which WKBJ solution is purely oscillatory. The exponentially growing solution on Stokes lines is called the dominant solution; the decaying solution on Stokes lines is called the sub-dominant/recessive solution. The sub-dominant solution will always becomes dominant in a neighboring Stokes line. However, the inverse is not true. (It may contain an amount of sub-dominant solution.) Each term changes from dominant to subdominant, or the reverse, when \(\zeta\) crosses an anti-Stokes line???

Even though we say “arbitrary”, the analytic solution in the whole complex plane possess a limit on that amount. The next question would be: how much exponentially decaying solution can you add to the exponentially growing solution? (Note that the asympotic series is also a divergent series: more terms don’t lead to high resolution accuracy! I have questions on this part???)
For the asymptotic approximation solution of Airy Equation 3.14, we need to define \(\arg(\zeta)\) properly to make it single value. Let us choose the branch cut \(-\pi\le\arg{\zeta}<\pi\). The complex plane is demonstrated in Figure 3.5.
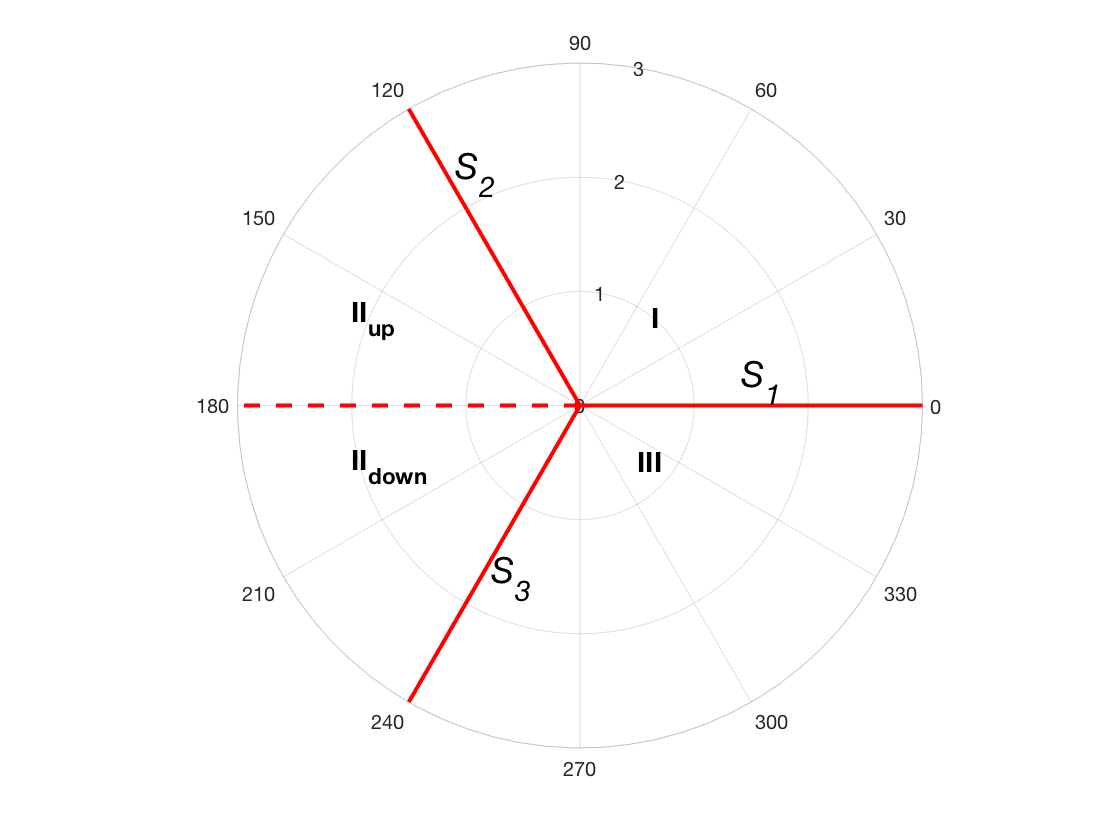
Let us start from region I. The solution in region I is
\[ E_I \sim \zeta^{-1/4}\big[ A_1 e^{-\frac{2}{3}\zeta^{3/2}} + B_1 e^{\frac{2}{3}\zeta^{3/2}}\big] \]
On \(S_1\), \(e^{-\frac{2}{3}\zeta^{3/2}}\) is sub-dominant, \(e^{\frac{2}{3}\zeta^{3/2}}\) is dominant. (The former would be dominant on neighboring Stokes lines \(S_2\) and \(S_3\).) Crossing \(S_2\) into region \(\text{II}_{\text{up}}\), we have
\[ E_{\text{II}_{\text{up}}} \sim \zeta^{-1/4} \Big[ \underbrace{A_1 e^{-\frac{2}{3}\zeta^{3/2}}}_{\text{dominant}} + \underbrace{(\lambda_1 A_1 + B_1)e^{\frac{2}{3}\zeta^{3/2}}}_{\text{sub-dominant}} \Big] \]
where \(\lambda_2\) is the Stokes constant on \(S_2\). The constant in the subdominant term has changed by \(\lambda_2 A_1\) because the differential equation is linear, and it cannot depend on \(B_1\). Otherwise it would be unaltered if we added to the solution in region I any multiple of the solution in which \(A_1=0\). (See (Budden 1961) 15.13.) Crossing the branch cut to region \(\text{II}_{\text{down}}\), \(\zeta^{\text{up}} = \zeta^{\text{down}}e^{i2\pi}\).
\[ \begin{aligned} \zeta_{\text{up}}^{-1/4} = \zeta_{\text{down}}^{-1/4}e^{i2\pi(-1/4)} = i\zeta_{\text{down}}^{1/4} \\ \zeta_{\text{up}}^{3/2} = \zeta_{\text{down}}^{3/2}e^{i2\pi(3/2)} = -\zeta_{\text{down}}^{3/2} \end{aligned} \]
so
\[ E_{\text{II}_{\text{down}}} = -i \zeta_{\text{II}_{\text{down}}}^{1/4}\Big[ A_1 e^{\frac{2}{3}\zeta_{\text{II}_{\text{down}}}^{3/2}} + (\lambda_2A_1 + B_1)e^{-\frac{2}{3}\zeta_{\text{II}_{\text{down}}}^{3/2}} \Big] \]
We can also go clockwise from I to III, crossing \(S_1\),
\[ E_{III} \sim \zeta^{-1/4} \Big[ \underbrace{B_1 e^{\frac{2}{3}\zeta^{3/2}}}_{\text{dominant}} + \underbrace{(-\lambda_1 B_1 + A_1)e^{-\frac{2}{3}\zeta^{3/2}}}_{\text{sub-dominant}} \Big] \]
where \(\lambda_1\) is the Stokes constant on \(S_1\), and the minus sign indicates the clockwise direction.
Crossing \(S_3\) from III to \(\text{II}_{\text{down}}\),
\[ E_{\text{II}_{\text{down}}} \sim \zeta^{-1/4} \Big[ \underbrace{(-\lambda_1B_1+A_1) e^{-\frac{2}{3}\zeta^{3/2}}}_{\text{dominant}} + \underbrace{ [(-\lambda_3)(-\lambda_1 B_1+A_1)+B_1]e^{\frac{2}{3}\zeta^{3/2}}}_{\text{sub-dominant}} \Big] \]
where \(\lambda_3\) is the Stokes constant on \(S_3\), and the minus sign indicates the clockwise direction.
Since the solution to Airy Equation is analytic, the solutions in region \(\text{II}_{\text{down}}\) obtained from two directions must be equal. Therefore
\[ \begin{aligned} -\lambda_1 B_1 + A_1 &= -i(\lambda_2 A_1 + B_1) \\ -\lambda_3 (-\lambda_1 B_1 + A_1) + B_1 &= -i A_1 \end{aligned} \]
\[ \begin{aligned} \begin{pmatrix} i\lambda_2 + 1 & -\lambda_1 + i \\ -\lambda_3 + i & \lambda_3\lambda_1 + 1 \end{pmatrix} \begin{pmatrix} A_1 \\ B_1 \end{pmatrix} = 0 \\ \Rightarrow \lambda_1 = \lambda_2 = \lambda_3 = i \end{aligned} \]
All three Stokes constants are \(i\). For the Airy equation, the amount of exponentially decaying solution you can have going from one Stokes line to another is restricted to \(i\) in counter-clockwise direction.
3.11.4 Application of Stokes Lines
Ex.1 Reflection Coefficient from Stokes Constant ???
Ex.2 O-mode
For EM O-mode wave in a non-magnetized plasma, the governing Equation 3.12 is rewritten here
\[ \frac{\mathrm{d}^2 E}{dz^2} +k^2 E = 0,\quad k^2 = \frac{\omega^2}{c^2}\Big[ 1-\frac{{\omega_p}^2(z)}{\omega^2} \Big] \]
Let the turning point be \(z=z_t\). Near \(z_t\), let \(k^2(z)=-p^2(z)(z-z_t)\) (Figure 3.3), where \(p(z)\) is real and positive for all real \(z\). Then
\[ k=\pm i p(z)(z-z_t)^{1/2} \]
In the following we need to choose sign s.t. \(k\) is real and positive on the anti-Stokes line \(AS_1\). (The figure of complex z plane is the same as Figure 3.5 except that the center point is \(z=z_t\). \(AS_1\) is the dashed line.)
To make \(z\) single value, define \(-\pi\le\arg{(z-z_t)}<\pi\). On \(AS_1\),
\[ \begin{aligned} k &= \pm ip(z)|z-z_t|^{1/2} e^{i\frac{\pi}{2}} \\ &=\mp|p(z)(z-z_t)|^{1/2} \\ &=\mp |k| \end{aligned} \]
We choose the second sign for right propagating wave, which has
\[ k=-ip(z)(z-z_t)^{1/2} \]
The sign is important here because it determines the propagation direction.
For \(z\) on \(S_1\), \(\arg{(z-z_t)} = 0\).
\[ k=-ip(z)|z-z_t|^{1/2}e^{i\frac{1}{2}0}=-i|k| \]
In region I (between \(S_1\) and \(S_2\))
\[ E_I \sim \frac{1}{\sqrt{k}}e^{-i\omega t\pm i\int_{z_t}^{z}kdz^\prime}\sim \frac{1}{\sqrt{k}}e^{-i\omega t\pm \int_{z_t}^z |k|dz^\prime} \]
For a decaying (subdominant) solution we must use minus (lower) sign, so
\[ E_I \sim E_{S_1} \sim \frac{1}{\sqrt{k}}e^{-i\omega t- \int_{z_t}^z kdz^\prime} \]
Crossing \(S_2\) into region \(II_{up}\),
\[ E_{S_2} \sim\frac{1}{\sqrt{k}}e^{-i\omega t}\Big[ \underbrace{e^{-i\int_{z_t}^z k dz^\prime}}_{\text{dominant on } S_2} + \underbrace{i e^{i\int_{z_t}^z kdz^\prime}}_{\text{sub-dominant on }S_2} \Big] = E_{AS_1} \]
where the first term represents the reflected wave, and the second term represents the incident wave. Since the magnitude of the incident and reflected wave is the same, the reflection coefficient should be 1, and the absorption coefficient should be 0. (In fact, there is a transmitted wave that is exponentially decay. WKBJ method cannot resolve this exponentially small value.)
Ex.3 Bohr-Sommerfield Quantization Rule
This is the classical potential well problem, where the two boundaries are \(z=z_1\) and \(z=z_2\).

Schrödinger equation reads
\[ \frac{\mathrm{d}^2\Psi}{dz^2} - \frac{2m}{{\hbar}^2}\big[ E-V(z)\big]\Psi = 0 \]
Imagine there is an potential well between \(z_1\) and \(z_2\) shown in Figure 3.6: what are the allowable energy state?
In this case, \(k^2 = -\frac{2m}{{\hbar}^2}\big[ E-V(z)\big]\). Wave travelling to the right has positive \(k(z)\), while wave travelling to the left has negative \(k(z)\). Following the discussion of reflection coefficient,
\[ \begin{aligned} R = i e^{-2i \int_{0}^{z_2}k(z^\prime)dz^\prime} \\ R^\prime = i e^{+2i \int_{0}^{z_1}k(z^\prime)dz^\prime} \end{aligned} \]
For waves bouncing back and forth inside the well, we must have
\[ \begin{aligned} RR^\prime = 1 \\ \Rightarrow (-1)e^{-2i \int_{z_1}^{z_2}kdz^\prime} = 1 \\ \Rightarrow \int_{z_1}^{z_2}k(z^\prime)dz^\prime = \pi (n+\frac{1}{2}),\ n=0,1,2,3,... \end{aligned} \]
which is called the Bohr-Sommerfield quantization rule.
Another way to do this problem is by recognizing the Stokes and anti-Stokes lines in the complex z plane and match the solution in the whole domain. Figure needed!!! As the opposite in HW8.1%k2 .vs. z , Stokes line
\[ k^2 = -\frac{2m}{{\hbar}^2}\big[ E-V(z)\big] \equiv -p^2(z)(z-z_1)(z-z_2) \]
where for large z, we must choose a minus sign in front of \(p(z)\) for \(p(z)\) to be real and positive. So
\[ k = \pm i p(z)(z-z_1)^{1/2}(z-z_2)^{1/2} \]
Then for a single-value solution, pick
\[ \begin{aligned} -\pi\le\arg{(z-z_1)}<\pi \\ -\frac{\pi}{2}\le\arg{(z-z_2)}<\frac{3\pi}{2} \end{aligned} \]
For \(z\) on \(AS_1\),
\[ k(z) = \pm ip(z)|z-z_1|^{1/2} e^{i\frac{1}{2}\cdot0}\cdot |z-z_2|^{1/2}e^{i\frac{1}{2}\cdot \pi} = \pm i |k|e^{i\frac{1}{2}\pi} = \mp |k| \]
For a real and positive \(k\) (right-traveling wave), we must choose the lower sign \(+\), so
\[ k =- i p(z)(z-z_1)^{1/2}(z-z_2)^{1/2} \]
For \(z\) on \(S_1\), \[ k =- i p(z)|z-z_1|^{1/2}|z-z_2|^{1/2}= -i |k| \]
For \(z\) on \(S_4\),
\[ k =- i p(z)|z-z_1|^{1/2}e^{i\frac{1}{2}\pi}|z-z_2|^{1/2}e^{i\frac{1}{2}\pi}= i |k| \]
So
\[ k(z) = \begin{cases} -i|k| & z>z_2 \\ |k| & z_1<z<z_2 \\ i|k| & z<z_1 \end{cases} \tag{3.19}\]
On \(S_1\),
\[ \Psi_{E_{S_1}} \sim \frac{1}{\sqrt{k}}e^{\pm i \int_{z_2}^{z} kdz^\prime} = \frac{1}{\sqrt{k}}e^{-i\int_{z_2}^{z}kdz^\prime} \]
such that this is sub-dominant on \(S_1\) (\(k=-i|k|\)).
Crossing \(S_2\) into region I, we have
\[ \Psi_I \sim \frac{1}{\sqrt{k}}\Big\{ \underbrace{e^{-i\int_{z_2}^z kdz^\prime}}_{\text{dominant on }S_2} + i\underbrace{e^{+i\int_{z_2}^z kdz^\prime}}_{\text{subdominant on }S_2} \Big\} \tag{3.20}\]
On \(S_4\),
\[ \Psi_{S_4}\sim \frac{1}{\sqrt{k}}e^{\pm i \int_{z_1}^z kdz^\prime} \sim \frac{1}{\sqrt{k}}e^{-i\int_{z_1}^z kdz^\prime}, \]
where minus sign is chosen s.t. it is subdominant on \(S_4\).
Crossing \(S_3\) into region I in the clockwise direction, we have
\[ \begin{aligned} \Psi_I &\sim \Big\{ \underbrace{e^{-i\int_{z_1}^z kdz^\prime}}_{\text{dominant on }S_3} - i\underbrace{e^{+i\int_{z_1}^z kdz^\prime}}_{\text{subdominant on }S_3} \Big\} \\ &= \frac{1}{\sqrt{k}}\Big\{ e^{-i\int_{z_2}^z kdz^\prime}\cdot e^{-i\int_{z_1}^{z_2}kdz^\prime} - ie^{i\int_{z_2}^z kdz^\prime}\cdot e^{i\int_{z_1}^{z_2}kdz^\prime} \Big\} \end{aligned} \tag{3.21}\]
Because the solution is analytic, Equation 3.20 and Equation 3.21 should be equal, therefore
\[ \begin{aligned} &\frac{1}{e^{-i\int_{z_1}^{z_2}kdz^\prime}} = \frac{i}{-ie^{i\int_{z_1}^{z_2}kdz^\prime}} \\ \Rightarrow& e^{2i\int_{z_1}^{z_2}kdz^\prime} = -1 = e^{i(\pi+2n\pi)},\quad n=0,1,2,3,... \\ \Rightarrow& \int_{z_1}^{z_2}kdz^\prime = (\frac{1}{2}+n)\pi,\quad n=0,1,2,3,... \end{aligned} \]
Ex.4 Tunneling Problem
Instead of a potential well, now we consider another classical tunneling problem, where \(E>V\) if \(z_1<z<z_2\).
\[ k^2(z) = \pm p^2(z)(z-z_1)(z-z_2) = p^2(z)(z-z_1)(z-z_2) \]
where the plus sign is chosen s.t. \(p(z)\) is real and positive for all real z, and then
\[ k = p(z)(z-z_1)^{1/2}(z-z_2)^{1/2} \]
Define arguments as follows
\[ 0\le \arg{z-z_2} < 2\pi,\quad -\pi<\arg{z-z_1} \le \pi \]
to remove the ambiguity in the branch in the expression of \(k\).
Since \(z=z_1\), \(z=z_2\) are simple turning points (with different slope in linear approximation), the Stokes and anti-Stokes lines are shown in Figure needed!!!
The branch cut defined as above give the following values of \(k\) on the real \(z\) axis:
\[ k(z) = \begin{cases} |k| & z>z_2 \\ i|k| & z_1<z<z_2 \\ -|k| & z<z_1 \end{cases} \tag{3.22}\]
On \(AS_1\), the solution
\[ E\sim \frac{1}{\sqrt{k}}e^{-i\omega t+i \int_{z_2}^z kdz^\prime} \tag{3.23}\]
represents the outgoing wave propagating to \(z=\infty\).
On \(S_2\), solution Equation 3.23 behaves like \(E\sim e^{\int_b^z |k|dz^\prime}\) which is dominant on \(S_2\) with respect to \(z=z_2\). Thus, on \(S_1\), it is subdominant.
On crossing \(S_1\) from \(AS_1\), solution Equation 3.23 remains valid. In fact, it is valid in the region bounded by \(S_1\), \(S_2\) and \(S_3\). Note that it is subdominant on \(S_2\) with respect to \(z=z_1\) (because we just showed that it is dominant on \(S_2\) with respect to \(z=z_2\)). Thus, we rewrite the solution as
\[ E\sim \frac{1}{\sqrt{k}}e^{-i\omega t + i\int_{z_2}^{z_1} kdz^\prime}\cdot \underbrace{e^{i\int_{z_1}^z kdz^\prime}}_{\text{subdominant on }\ S_2 w.r.t\ z=a} \]
which becomes dominant on \(S_3\). Upon crossing \(S_3\), this solution becomes
\[ E\sim \frac{1}{\sqrt{k}}e^{-i\omega t + i\int_{z_2}^{z_1} kdz^\prime} \big[ \underbrace{e^{i\int_{z_1}^z kdz^\prime}}_{\text{dominant on }S_3} + \underbrace{ie^{-i\int_{z_1}^z kdz^\prime}}_{\text{subdominant on }S_3} \big] \]
where we pick up the Stokes constant \(i\) and the subdominant solution, represented by the last term of the solution.
Now, this is the solution on \(AS_4\) (\(z<z_1\)). Referring to Equation 3.22, we see that the first term of the solution represents the reflected wave, and the second term the incident wave from \(z=-\infty\). Since the incident wave and reflected wave have equal amplitude, we have
\[ |R|^2 = 1 \]
The transmitted wave has unit amplitude (see Eq.(\(\ref{eq-tunnel_AS1}\))). The incident wave has amplitude \(e^{i\int_a^b kdz^\prime}(i)\). Thus,
\[ |T|^2 = \frac{1}{\big| e^{i\int_{z_1}^{z_2} kdz^\prime}(i) \big|^2} = \frac{1}{\big| e^{i\int_{z_1}^{z_2} i|k|dz^\prime}(i) \big|^2} = e^{-2\int_{z_1}^{z_2} |k|dz} \]
where \(z_1,z_2\) are far apart, i.e. \(|T|^2\) is exponentially small.
Note: \(|R|\) and \(|T|\) above are not valid if \(z_1,z_2\) are close to each other. The correct transmission coefficient, for general valies of \(z_1,z_2\) is
\[ |T|^2 = \frac{e^{-2\int_{z_1}^{z_2} |k|dz}}{1+e^{-2\int_{z_1}^{z_2} |k|dz}} \]
and the reflection coefficient is
\[ |R|^2 = 1- |T|^2 \]
Ex.5 Two waves: one is launched from \(z=+\infty\), incident onto a resonant layer at \(z=a (a>0)\), and the other launched from \(z=-\infty\), incident onto a absorption layer at \(z=0\), with the model equation
\[ \frac{\mathrm{d}^2 E(z)}{dz} + {k_0}^2 \Big( \frac{z}{z-a}\Big) E(z) = 0 \]
This looks like a similar case for ECRH.
\[ k^2(z) = {k_0}^2 \Big( \frac{z}{z-a}\Big) \Rightarrow k(z) = k_0 z^{1/2}(z-a)^{-1/2} \]
where \(k_0\) is real and positive.
Define arguments as follows
\[ -\frac{3\pi}{2}\le \arg{z} < \frac{\pi}{2},\quad -\frac{3\pi}{2}<\arg{z-a} \le \frac{\pi}{2} \]
to remove the ambiguity in the branch in the expression of \(k\).
For \(z\) on \(AS_1\),
\[ k = k_0 |z|^{1/2}e^{-\frac{1}{2}0}|z-a|^{-1/2}e^{i\frac{1}{2}0} = |k| \]
For \(z\) on \(S_1\),
\[ k = k_0 |z|^{1/2}e^{-\frac{1}{2}0}|z-a|^{-1/2}e^{i\frac{1}{2}\pi} = i|k| \]
For \(z\) on \(AS_2\),
\[ k = k_0 |z|^{1/2}e^{i\frac{1}{2}(-\pi)}|z-a|^{-1/2}e^{i\frac{-1}{2}(-\pi)} = |k| \]
Then the branch cut defined as above give the following values of \(k\) on the real \(z\) axis:
\[ k(z) = \begin{cases} |k| & z>a \\ i|k| & 0<z<a \\ |k| & z<0 \end{cases} \tag{3.24}\]
For wave launched from large magnetic field side \(z=+\infty\) going to \(z=-\infty\) on \(AS_3\), the solution on \(AS_3\) is (Note that even though \(z\) is negative, it is the upper limit of the integral and k is positive. It took me a long time to get the right sign here for a left propagating wave.)
\[ E\sim \frac{1}{\sqrt{k}}e^{-i\omega t- i \int_0^z kdz^\prime} \] This solution behaves like
\[ E\sim \frac{1}{\sqrt{k}} e^{-i\omega t- i \int_0^z i|k|dz^\prime} \sim \frac{1}{\sqrt{k}} e^{-i\omega t + \int_0^z |k|dz^\prime} \tag{3.25}\]
on \(S_1\). Thus, it is dominant on \(S_1\) with respect to \(z=0\); it is subdominant on the neighboring Stokes line \(S_2\). Thus solution Equation 3.25 remains valid upon crosing Stokes line \(S_2\). It is the solution in region I, bounded by \(S_1\) and \(S_2\). Since it is dominant on \(S_1\) with respect to \(z=0\), it is subdominant on \(S_1\) with respect to \(z=a\). So we can write it as
\[ E \sim \frac{1}{\sqrt{k}}e^{-i\omega t - i\int_0^a kdz^\prime}\cdot \underbrace{e^{-i\int_a^z kdz^\prime}}_{\text{subdominant on }\ S_1\ w.r.t.\ z=a} \]
which is also the incident wave from \(z=0\). This is the solution in region I as well as on \(AS_1\) (\(k=|k|\)). So it is the incident wave solution from \(z=\infty\). The reflection coefficient must be 0!
The transmisson coefficient is then
\[ \begin{aligned} |T|^2 &= \Big| \frac{E(z=-\infty)}{E(z=\infty)} \Big|^2 = \frac{1}{|e^{-i\int_0^a kdz}|^2} \notag \\ &= e^{-2\int_0^a |k| dz} = e^{-2\int_0^a k_0 \sqrt{\frac{z}{a-z}}dz} \end{aligned} \]
Let \(z=a\sin^2\theta\), we can finally have
\[ |T|^2 = e^{-k_0 a\pi} \]
The fraction of power absorbed by resonance is
\[ 1-|R|^2 - |T|^2 = 1-e^{-k_0 a \pi} \]
Note: these expressions of \(|T|^2, \ |R|^2\) are valid even if \(a\) is small.
For wave launched from low magnetic field side \(z=-\infty\),
\[ E_{AS_1} \sim\frac{1}{\sqrt{k}}e^{-i\omega t + i \int_a^z kdz^\prime} \]
On \(S_1\), a subdominant (decaying) solution with respect to \(z=0\) is
\[ E_{S_1}\sim \frac{1}{\sqrt{k}}e^{-i\omega t+i\int_0^z i|k|dz^\prime} \]
In regions I bounded by \(S_1,\ S_2\) and \(AS_1\),
\[ E_I \sim E_{S_1}\frac{1}{\sqrt{k}}e^{i\int_a^0 kdz^\prime}\cdot e^{i\int_0^z kdz^\prime} \]
\(E_{S_1}\) is dominant on \(S_1\) with respect to \(z=a\), but is subdominant on \(S_1\) with respect to \(z=0\).
Crossing \(S_2\) into \(AS_2\),
\[ E_{AS_2}\sim \frac{1}{\sqrt{k}}e^{-i\omega t}\cdot e^{i\int_a^0 kdz^\prime}\Big[ \underbrace{e^{i\int_0^z kdz^\prime}}_{\text{dominant on }S_3} - i \underbrace{e^{-i\int_0^z kdz^\prime}}_{\text{subdominant on }S_3} \Big], \]
where the first term represents the reflected wave, and the second term represents the incident wave.
The transmission coefficient is
\[ \begin{aligned} T &= \Big| \frac{E(z=\infty)}{E(z=-\infty)} \Big| \\ &=\Big|\frac{\sqrt{k(-\infty)}}{\sqrt{k(\infty)}} \Big| \Big| \frac{e^{i\int_a^\infty kdz}}{e^{i\int_a^0 kdz}\cdot e^{i\int_0^{-\infty} kdz}} \Big| \\ &=\frac{1}{\big| e^{i\int_a^0 i|k|dz} \big|} = e^{-\int_0^a |k|dz} \end{aligned} \]
Then the transmission coefficient in power is
\[ T^2 = e^{-2\int_0^a k \sqrt{|\frac{z}{z-a}|}dz^\prime } = e^{-k_0 a \pi} \]
where the last equivalence requires some transformation tricks. If \(a\sim\lambda, k_0 = 2\pi/\lambda\), the transmitted power fraction is on the order of \(e^{-20}\sim 10^{-9}\).
The reflection coefficient is zero and that the transmission coefficient (in power) is \(T=e^{-k_0 a\pi}\). Thus, the fraction \(1-T\) of the incident power is absorbed by that resonant layer.
3.11.5 “Exact” WKBJ Solution
- Shielding or tunneling
If you have a high density region between \(x_1\) and \(x_2\),
\[ k^2(x) = \frac{\omega^2}{c^2}\big[ 1-\frac{{\omega_p}^2(x)}{\omega^2}\big] \]
The transmission coefficient in power is
\[ |T|^2 = \frac{e^{-2\int_{x_1}^{x_2}|k|\mathrm{d}x}}{1+e^{-2\int_{x_1}^{x_2}|k|\mathrm{d}x}} \]
and the reflection coefficient in power is
\[ |R|^2 = \frac{1}{1+e^{-2\int_{x_1}^{x_2}|k|\mathrm{d}x}} \]
Note:
\(|R|^2+|T|^2 = 1\)
When \(x_1=x_2\), i.e. \(\omega^2 = {\omega_p}^2(\text{peak})\), \(|R|^2=|T|^2=\frac{1}{2}\).
ECRH
\[ \frac{\mathrm{d}^2E}{dz^2} + {k_0}^2\Big( \frac{z}{z-a}\Big)E = 0 \]
where
\[ k^2(z) = {k_0}^2\Big( \frac{z}{z-a}\Big) \]
- Incident wave from \(z=-\infty\) (from low \(B_0\) side)
\[ \begin{aligned} |R| &= 1 - e^{-\pi k_0 a} \\ |T| &= e^{-\frac{1}{2}\pi k_0 a} \\ |R|^2 + |T|^2 &= 1-e^{-\pi k_0 a} + e^{-2\pi k_0 a} <1 \end{aligned} \]
- Incident wave from \(z=\infty\)
\[ \begin{aligned} |R| &= 0 \\ |T| &= e^{-\pi k_0 a/2} \\ |R|^2 + |T|^2 &= e^{-\pi k_0 a} < 1 \end{aligned} \]
which means almost perfect absorption at \(z=a\).
Note: These formulas are valid even if \(a\rightarrow0\), in which limit \(|R|\rightarrow 0,\ |T|\rightarrow 1\), for both (I) and (II), as expected from the model equation.
Singularity in refractive index \(n\) can lead to absorption, even without collision.
3.12 Normalization
In physics we frequently have to deal with unit conversions. A solid understanding of the unit system and normalization methods paves the path for understanding the scales behind systems.
3.13 Wavelet Analysis
Wavelet Transform (WT) decomposes a function into a set of wavelets. A Wavelet is a wave-like oscillation that is localized in time. Two basic properties of a wavelet are scale and location.
Wavelet is a predecessor of Fourier Tranform (FT), which provides better results when dealing with changing background. It is the de-facto method for modern wave analysis. The key advantages of WT compared with FT are:
- Fewer “hard” parameters to tune in WT. For example, if you want to make a spectrogram with FT, you need to specify the size of local DFTs. In WT you do not need to worry about this; instead the validity of the result can be shown by the cone of influence. In a sense, FT makes immediate conversion from time to frequency domain, while WT let you choose the intermediate steps you wish for.
- Flexible forms of wavelets to choose from. In practice, if you have any prior knowledge to the signal you want to identify, you can find for an appropriate wavelet that is close to that shape, which gives better fitting compared to the sinuisoidal functions in FT.
Check the notes from my blog and the references therein.